Coin rotation paradox

Short description: Geometry problem of a coin rolling around another coin.

The outer coin makes two rotations rolling once around the inner coin.

The path of a single point on the edge of the moving coin is a cardioid.

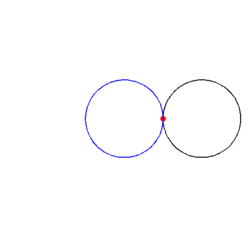
The coin rotation paradox is the counter-intuitive math problem that, when one coin is rolled around the rim of another coin of equal size, the moving coin completes not one but two full rotations after going all the way around the stationary coin, when viewed from an external reference frame. The problem can be generalized to coins of different radii; in another form, it appeared in an SAT test but none of the multiple choice answers allowed were correct.

Description

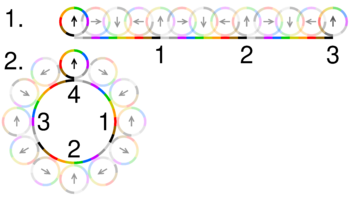
Start with two identical coins touching each other on a table, with their "head" sides displayed and parallel. Keeping coin A stationary, rotate coin B around A, keeping a point of contact with no slippage. As coin B reaches the opposite side, the two heads will again be parallel; B has made one revolution. Continuing to move B brings it back to the starting position and completes a second revolution. Paradoxically, coin B appears to have rolled a distance equal to twice its circumference. In reality, as the circumferences of both coins are equal, by definition coin B has only rolled a distance equal to its own circumference. The second rotation arises from the fact that the path along which it has rolled is a circle. This is analogous to simply rotating coin B "in situ".

One way to visualize the effect is to imagine the circumference of coin A "flattened out" into a straight line, by which means it can be observed that coin B has rotated only once as it travels along its, now flat, path. This is the "first rotation". Equally, sliding coin B around the circumference of coin A, instead of rolling it, whilst maintaining its current specific point of contact, will impart a rotation representative of the "second rotation" in the original scenario.

As coin B rotates, each point on its perimeter describes (moves through) a cardioid curve.

Analysis and solution

From start to end, the center of the moving coin travels a circular path. The circumference of the stationary coin and the path of the centre form two concentric circles. The radius of the outer circle is the sum of the coins' radii; hence, the circumference of the path of the moving centre is twice either coin's circumference. The center of the moving coin travels twice the coin's circumference without slipping; therefore, the moving coin makes two complete revolutions.

How much the moving coin rotates around its own center en route, if any, or in what direction – clockwise, counterclockwise, or some of both – has no effect on the length of the path. That the coin rotates twice as described above and focusing on the edge of the moving coin as it touches the stationary coin are distractions.

Unequal radii and other shapes

Example where R = 3r. In figure 1, with R straightened out, the number of rotations (number of times the arrow subsequently points upward) is R/r = 3. In figure 2, as R has been restored into a circle, the coin makes an extra rotation, giving R/r + 1 = 4. (Animation)

Rotation of a small coin around a larger one

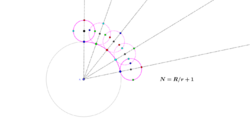
A coin of radius r rolling around one of radius R makes R/r + 1 rotations. That is because the center of the rolling coin travels a circular path with a radius (or circumference) of R + r/r = R/r + 1 times its own radius (or circumference). In the limiting case when R = 0, the coin with radius r makes 0/r + 1 = 1 simple rotation around its bottom point.

The May 1, 1982, SAT had a question concerning this problem, and, due to human error, had to be regraded after three students proved there was no correct answer among the choices.

The shape around which the coin is rolled need not be a circle: one extra rotation is added to the ratio of their perimeters when it is any simple polygon or closed curve which does not intersect itself. If the shape is complex, the number of rotations added (or subtracted, if the coin rolls inside the curve) is the absolute value of its turning number.

Applications

The paradox is related to sidereal time: a sidereal day is the time Earth takes to rotate for a distant star to return to the same position in the sky, whereas a solar day is the time for the sun to return to the same position. A year has around 365.25 solar days, but 366.25 sidereal days to account for one revolution around the sun. As a solar day has 24 hours, a sidereal day has around 365.25/366.25 × 24 hours = 23 hours, 56 minutes and 4.1 seconds.

A version of the puzzle arises in group theory, specifically the study of the Lie group known as the split real form of G₂. One construction of this group uses the fact that a ball rolling around another ball with three times its radius will make four full turns, rather than three.

See also

• Aristotle's wheel paradox

Further reading

• "Penny Puzzles". Mathematical Carnival. Alfred A. Knopf. 1975. 

External links

• Nguyen, Huyen (2020-06-04). "answer to the question What proven math fact surprised you the most...". https://www.quora.com/What-proven-math-fact-surprised-you-the-most-when-you-learned-it/answer/Huyen-Nguyen-111. 

This upvoted answer includes animations and intuitive explanations about the original question where r of the "outer coin" was 1/3 of the inner coin's radius.

• Muller, Derek (2023-11-30). "The SAT Question Everyone Got Wrong" (url). Veritasium. https://www.youtube.com/watch?v=FUHkTs-Ipfg.