Collinearity equation

Short description: Two equations relating 2D sensor plane coordinates to 3D object coordinates

Light beams passing through the pinhole of a pinhole camera

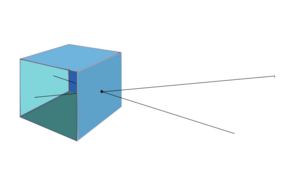
The collinearity equations are a set of two equations, used in photogrammetry and computer stereo vision, to relate coordinates in a sensor plane (in two dimensions) to object coordinates (in three dimensions). The equations originate from the central projection of a point of the object through the optical centre of the camera to the image on the sensor plane.

The three points P, Q and R are projected on the plane S through the projection centre C

x- and z-axis of the projection of P through the projection centre C

Definition

Let x,y, and z refer to a coordinate system with the x- and y-axis in the sensor plane. Denote the coordinates of the point P on the object by [math]\displaystyle{ x_P,y_P,z_P }[/math], the coordinates of the image point of P on the sensor plane by x and y and the coordinates of the projection (optical) centre by [math]\displaystyle{ x_0,y_0,z_0 }[/math]. As a consequence of the projection method there is the same fixed ratio [math]\displaystyle{ \lambda }[/math] between [math]\displaystyle{ x-x_0 }[/math] and [math]\displaystyle{ x_0-x_P }[/math], [math]\displaystyle{ y-y_0 }[/math] and [math]\displaystyle{ y_0-y_P }[/math], and the distance of the projection centre to the sensor plane [math]\displaystyle{ z_0=c }[/math] and [math]\displaystyle{ z_P-z_0 }[/math]. Hence:

[math]\displaystyle{ x-x_0=-\lambda (x_P-x_0) }[/math]

[math]\displaystyle{ y-y_0=-\lambda (y_P-y_0) }[/math]

[math]\displaystyle{ c=\lambda (z_P-z_0), }[/math]

Solving for [math]\displaystyle{ \lambda }[/math] in the last equation and entering it in the others yields:

[math]\displaystyle{ x-x_0=-c\ \frac{x_P-x_0}{z_P-z_0} }[/math]

[math]\displaystyle{ y-y_0=-c\ \frac{y_P-y_0}{z_P-z_0} }[/math]

The point P is normally given in some coordinate system "outside" the camera by the coordinates X, Y and Z, and the projection centre by [math]\displaystyle{ X_0,Y_0,Z_0 }[/math]. These coordinates may be transformed through a rotation and a translation to the system on the camera. The translation doesn't influence the differences of the coordinates, and the rotation, often called camera transform, is given by a 3×3-matrix R, transforming [math]\displaystyle{ (X-X_0,Y-Y_0,Z-Z_0) }[/math] into:

[math]\displaystyle{ x_P-x_0=R_{11} (X-X_0)+ R_{21}(Y-Y_0) + R_{31} (Z-Z_0) }[/math]

[math]\displaystyle{ y_P-y_0=R_{12} (X-X_0)+ R_{22}(Y-Y_0) + R_{32} (Z-Z_0) }[/math]

and

[math]\displaystyle{ z_P-z_0=R_{13}(X-X_0) + R_{23} (Y-Y_0) + R_{33} (Z-Z_0) }[/math]

Substitution of these expressions, leads to a set of two equations, known as the collinearity equations:

[math]\displaystyle{ x - x_0= -c\ \frac{R_{11} (X-X_0)+ R_{21}(Y-Y_0) + R_{31} (Z-Z_0)} {R_{13}(X-X_0) + R_{23} (Y-Y_0) + R_{33} (Z-Z_0)} }[/math]

[math]\displaystyle{ y - y_0= -c\ \frac{R_{12} (X-X_0)+ R_{22}(Y-Y_0) + R_{32} (Z-Z_0)} {R_{13}(X-X_0) + R_{23} (Y-Y_0) + R_{33} (Z-Z_0)} }[/math]

The most obvious use of these equations is for images recorded by a camera. In this case the equation describes transformations from object space (X, Y, Z) to image coordinates (x, y). It forms the basis for the equations used in bundle adjustment. They indicate that the image point (on the sensor plate of the camera), the observed point (on the object) and the projection center of the camera were aligned when the picture was taken.

See also

• 3D projection
• Epipolar geometry
• Pinhole camera model