Constant chord theorem

Short description: Invariant cord in one of two intersecting circles based on any point in the other

constant chord length: [math]\displaystyle{ |P_1Q_1|=|P_2Q_2| }[/math]

constant diameter length: [math]\displaystyle{ |P_1Q_1|=|P_2Q_2| }[/math]

The constant chord theorem is a statement in elementary geometry about a property of certain chords in two intersecting circles.

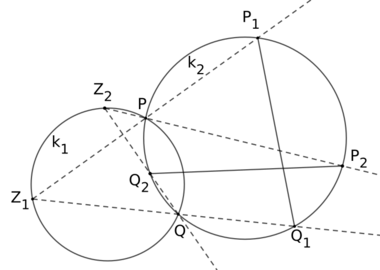
The circles [math]\displaystyle{ k_1 }[/math] and [math]\displaystyle{ k_2 }[/math] intersect in the points [math]\displaystyle{ P }[/math] and [math]\displaystyle{ Q }[/math]. [math]\displaystyle{ Z_1 }[/math] is an arbitrary point on [math]\displaystyle{ k_1 }[/math] being different from [math]\displaystyle{ P }[/math] and [math]\displaystyle{ Q }[/math]. The lines [math]\displaystyle{ Z_1P }[/math] and [math]\displaystyle{ Z_1Q }[/math] intersect the circle [math]\displaystyle{ k_2 }[/math] in [math]\displaystyle{ P_1 }[/math] and [math]\displaystyle{ Q_1 }[/math]. The constant chord theorem then states that the length of the chord [math]\displaystyle{ P_1Q_1 }[/math] in [math]\displaystyle{ k_2 }[/math] does not depend on the location of [math]\displaystyle{ Z_1 }[/math] on [math]\displaystyle{ k_1 }[/math], in other words the length is constant.

The theorem stays valid when [math]\displaystyle{ Z_1 }[/math] coincides with [math]\displaystyle{ P }[/math] or [math]\displaystyle{ Q }[/math], provided one replaces the then undefined line [math]\displaystyle{ Z_1P }[/math] or [math]\displaystyle{ Z_1Q }[/math] by the tangent on [math]\displaystyle{ k_1 }[/math] at [math]\displaystyle{ Z_1 }[/math].

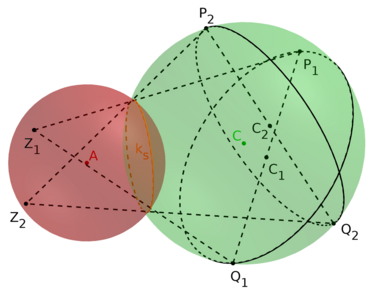
A similar theorem exists in three dimensions for the intersection of two spheres. The spheres [math]\displaystyle{ k_1 }[/math] and [math]\displaystyle{ k_2 }[/math] intersect in the circle [math]\displaystyle{ k_s }[/math]. [math]\displaystyle{ Z_1 }[/math] is arbitrary point on the surface of the first sphere [math]\displaystyle{ k_1 }[/math], that is not on the intersection circle [math]\displaystyle{ k_s }[/math]. The extended cone created by [math]\displaystyle{ k_s }[/math] and [math]\displaystyle{ Z_1 }[/math] intersects the second sphere [math]\displaystyle{ k_2 }[/math] in a circle. The length of the diameter of this circle is constant, that is it does not depend on the location of [math]\displaystyle{ Z_1 }[/math] on [math]\displaystyle{ k_1 }[/math].

Nathan Altshiller Court described the constant chord theorem 1925 in the article sur deux cercles secants for the Belgian math journal Mathesis. Eight years later he published On Two Intersecting Spheres in the American Mathematical Monthly, which contained the 3-dimensional version. Later it was included in several textbooks, such as Ross Honsberger's Mathematical Morsels and Roger B. Nelsen's Proof Without Words II, where it was given as a problem, or the German geometry textbook Mit harmonischen Verhältnissen zu Kegelschnitten by Halbeisen, Hungerbühler and Läuchli, where it was given as a theorem.

References

• Lorenz Halbeisen, Norbert Hungerbühler, Juan Läuchli: Mit harmonischen Verhältnissen zu Kegelschnitten: Perlen der klassischen Geometrie. Springer 2016, ISBN:9783662530344, p. 16 (German)
• Roger B. Nelsen: Proof Without Words II. MAA, 2000, p. 29
• Ross Honsberger: Mathematical Morsels. MAA, 1979, ISBN:978-0883853030, pp. 126–127
• Nathan Altshiller Court: On Two Intersecting Spheres. The American Mathematical Monthly, Band 40, Nr. 5, 1933, pp. 265–269 (JSTOR)
• Nathan Altshiller-Court: sur deux cercles secants. Mathesis, Band 39, 1925, p. 453 (French)

External links

• constant chord theorem as problem at cut-the-knot.org