Cross-serial dependencies
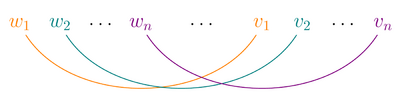
In linguistics, cross-serial dependencies (also called crossing dependencies by some authors[1]) occur when the lines representing the dependency relations between two series of words cross over each other.[2] They are of particular interest to linguists who wish to determine the syntactic structure of natural language; languages containing an arbitrary number of them are non-context-free. By this fact, Dutch[3] and Swiss-German[4] have been proven to be non-context-free.
Example
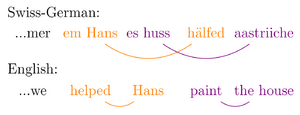
As Swiss-German allows verbs and their arguments to be ordered cross-serially, we have the following example, taken from Shieber:[4]
| ...mer | em Hans | es | huus | hälfed | aastriiche. |
| ...we | Hans (dat) | the | house (acc) | help | paint. |
That is, "we help Hans paint the house."
Notice that the sequential noun phrases em Hans (Hans) and es huus (the house), and the sequential verbs hälfed (help) and aastriiche (paint) both form two separate series of constituents. Notice also that the dative verb hälfed and the accusative verb aastriiche take the dative em Hans and accusative es huus as their arguments, respectively.
Non-context-freeness
Let [math]\displaystyle{ L_{SG} }[/math] to be the set of all Swiss-German sentences. We will prove mathematically that [math]\displaystyle{ L_{SG} }[/math] is not context-free.
In Swiss-German sentences, the number of verbs of a grammatical case (dative or accusative) must match the number of objects of that case. Additionally, a sentence containing an arbitrary number of such objects is admissible (in principle). Hence, we can define the following formal language, a subset of [math]\displaystyle{ L_{SG} }[/math]:[math]\displaystyle{ L =\text{De Jan} \text{ s}\ddot{\mathrm{a}}\text{it} \text{ das} \text{ mer} \text{ (d'chind)}{}^m \text{ (em} \text{ Hans)}{}^n \text{ s} \text{ huus} \text{ h}\ddot{\mathrm{a}}\text{nd} \text{ wele} \text{ (laa)}{}^m \text{ (h}\ddot{\mathrm{a}}\text{lfe)}{}^n \text{ aastriiche.} }[/math]Thus, we have [math]\displaystyle{ L = L_{SG} \cap L_r }[/math], where [math]\displaystyle{ L_r }[/math] is the regular language defined by [math]\displaystyle{ L =\text{De Jan} \text{ s}\ddot{\mathrm{a}}\text{it} \text{ das} \text{ mer} \text{ (d'chind)}{}^+ \text{ (em} \text{ Hans)}{}^+ \text{ s} \text{ huus} \text{ h}\ddot{\mathrm{a}}\text{nd} \text{ wele} \text{ (laa)}{}^+ \text{ (h}\ddot{\mathrm{a}}\text{lfe)}{}^+ \text{ aastriiche.} }[/math]where the superscript plus symbol means "one or more copies". Since the set of context-free languages is closed under intersection with regular languages, we need only prove that [math]\displaystyle{ L }[/math] is not context-free (,[5] pp 130–135).
After a word substitution, [math]\displaystyle{ L }[/math] is of the form [math]\displaystyle{ \{x a^m b^n y c^m d^n z | m, n \geq 1\} }[/math]. Since [math]\displaystyle{ L }[/math] can be mapped to [math]\displaystyle{ L' }[/math] by the following map: [math]\displaystyle{ x, y, z \mapsto \epsilon; a \mapsto a; b \mapsto b; c \mapsto c }[/math], and since the context-free languages are closed under mappings from terminal symbols to terminal strings (that is, a homomorphism) (,[5] pp 130–135), we need only prove that [math]\displaystyle{ L' }[/math] is not context-free.
[math]\displaystyle{ L' =\{ a^m b^n c^m d^n | m, n \geq 1\} }[/math] is a standard example of non-context-free language (,[5] p. 128). This can be shown by Ogden's lemma.
Suppose the language is generated by a context-free grammar, then let [math]\displaystyle{ p }[/math] be the length required in Ogden's lemma, then consider the word [math]\displaystyle{ a^pb^pc^pd^p }[/math] in the language, and mark the letters [math]\displaystyle{ b^pc^p }[/math]. Then the three conditions implied by Ogden's lemma cannot all be satisfied.
All known spoken languages which contain cross-serial dependencies can be similarly proved to be not context-free.[2] This led to the abandonment of Generalized Phrase Structure Grammar once cross-serial dependencies were identified in natural languages in the 1980s.[6]
Treatment
Research in mildly context-sensitive language has attempted to identify a narrower and more computationally tractable subclass of context-sensitive languages that can capture context sensitivity as found in natural languages. For example, cross-serial dependencies can be expressed in linear context-free rewriting systems (LCFRS); one can write a LCFRS grammar for {anbncndn | n ≥ 1} for example.[7][8][9]
References
- ↑ Stabler, Edward (2004), "Varieties of crossing dependencies: structure dependence and mild context sensitivity", Cognitive Science 28 (5): 699–720, doi:10.1016/j.cogsci.2004.05.002, http://www.linguistics.ucla.edu/people/stabler/Stabler04-Copying.pdf.
- ↑ 2.0 2.1 Jurafsky, Daniel; Martin, James H. (2000). Speech and Language Processing (1st ed.). Prentice Hall. pp. 473–495. ISBN 978-0-13-095069-7..
- ↑ Bresnan, Joan; M. Kaplan, Ronald (1982), "Cross-serial dependencies in Dutch", Linguistic Inquiry 13 (4): 613–635.
- ↑ 4.0 4.1 Shieber, Stuart (1985), "Evidence against the context-freeness of natural language", Linguistics and Philosophy 8 (3): 333–343, doi:10.1007/BF00630917, http://www.eecs.harvard.edu/~shieber/Biblio/Papers/shieber85.pdf.
- ↑ 5.0 5.1 5.2 John E. Hopcroft, Jeffrey D. Ullman (1979). Introduction to Automata Theory, Languages, and Computation (1st ed.). Pearson Education. ISBN 978-0-201-44124-6..
- ↑ Gazdar, Gerald (1988). "Applicability of Indexed Grammars to Natural Languages". Natural Language Parsing and Linguistic Theories. Studies in Linguistics and Philosophy. 35. pp. 69–94. doi:10.1007/978-94-009-1337-0_3. ISBN 978-1-55608-056-2.
- ↑ http://user.phil-fak.uni-duesseldorf.de/~kallmeyer/GrammarFormalisms/4nl-cfg.pdf[bare URL PDF]
- ↑ http://user.phil-fak.uni-duesseldorf.de/~kallmeyer/GrammarFormalisms/4lcfrs-intro.pdf[bare URL PDF]
- ↑ Laura Kallmeyer (2010). Parsing Beyond Context-Free Grammars. Springer Science & Business Media. pp. 1–5. ISBN 978-3-642-14846-0.
 |  |
