Dependency network

From HandWiki

The dependency network approach provides a system level analysis of the activity and topology of directed networks. The approach extracts causal topological relations between the network's nodes (when the network structure is analyzed), and provides an important step towards inference of causal activity relations between the network nodes (when analyzing the network activity). This methodology has originally been introduced for the study of financial data,[1][2] it has been extended and applied to other systems, such as the immune system,[3] and semantic networks.[4]

In the case of network activity, the analysis is based on partial correlations.[5][6][7][8][9] In simple words, the partial (or residual) correlation is a measure of the effect (or contribution) of a given node, say j, on the correlations between another pair of nodes, say i and k. Using this concept, the dependency of one node on another node is calculated for the entire network. This results in a directed weighted adjacency matrix of a fully connected network. Once the adjacency matrix has been constructed, different algorithms can be used to construct the network, such as a threshold network, Minimal Spanning Tree (MST), Planar Maximally Filtered Graph (PMFG), and others.

Dependency network of financial data, for 300 of the S&P500 stocks, traded between 2001–2003. Stocks are grouped by economic sectors, and the arrow points in the direction of influence. The hub of the network, the most influencing sector, is the Financial sector. Reproduction from Kenett et al., PLoS ONE 5(12), e15032 (2010)

Importance

The partial correlation based dependency network is a class of correlation network, capable of uncovering hidden relationships between its nodes.

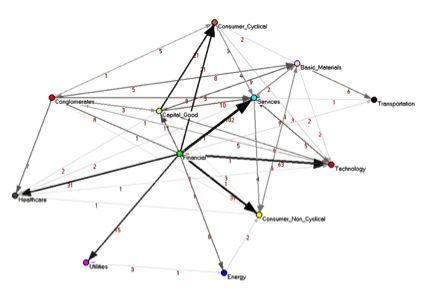
This original methodology was first presented at the end of 2010, published in PLoS ONE.[1] The authors quantitatively uncovered hidden information about the underlying structure of the U.S. stock market, information that was not present in the standard correlation networks. One of the main results of this work is that for the investigated time period (2001–2003), the structure of the network was dominated by companies belonging to the financial sector, which are the hubs in the dependency network. Thus, they were able for the first time to quantitatively show the dependency relationships between the different economic sectors. Following this work, the dependency network methodology has been applied to the study of the immune system,[3] and semantic networks.[4]

Dependency Network of specific antibodies activity, measured for a group of mothers. Panel (a) presents the dependency network, and panel (b) the standard correlation network. Reproduction from Madi et al., Chaos 21, 016109 (2011)
Example of Dependency Network of associations, constructed from a full semantic network. Reproduction from Kenett et al., PLoS ONE 6(8): e23912 (2011)

Overview

To be more specific, the partial correlation of the pair (i, k) given j, is the correlation between them after proper subtraction of the correlations between i and j and between k and j. Defined this way, the difference between the correlations and the partial correlations provides a measure of the influence of node j on the correlation. Therefore, we define the influence of node j on node i, or the dependency of node i on node j − D(i,j), to be the sum of the influence of node j on the correlations of node i with all other nodes.

In the case of network topology, the analysis is based on the effect of node deletion on the shortest paths between the network nodes. More specifically, we define the influence of node j on each pair of nodes (i,k) to be the inverse of the topological distance between these nodes in the presence of j minus the inverse distance between them in the absence of node j. Then we define the influence of node j on node i, or the dependency of node i on node j − D(i,j), to be the sum of the influence of node j on the distances between node i with all other nodes k.

The activity dependency networks

The node-node correlations

The node-node correlations can be calculated by Pearson’s formula:

[math]\displaystyle{ C_{i,j}=\frac {\left \langle (X_i (n)- \mu_i) (X_j (n)- \mu_j)\right \rangle}{\sigma_i \sigma_j} }[/math]

Where [math]\displaystyle{ X_i(n) }[/math] and [math]\displaystyle{ X_j(n) }[/math] are the activity of nodes i and j of subject n, μ stands for average, and sigma the STD of the dynamics profiles of nodes i and j. Note that the node-node correlations (or for simplicity the node correlations) for all pairs of nodes define a symmetric correlation matrix whose [math]\displaystyle{ (i,j) }[/math] element is the correlation between nodes i and j.

Partial correlations

Next we use the resulting node correlations to compute the partial correlations. The first order partial correlation coefficient is a statistical measure indicating how a third variable affects the correlation between two other variables. The partial correlation between nodes i and k with respect to a third node [math]\displaystyle{ j - PC(i,k\mid j) }[/math] is defined as:

[math]\displaystyle{ PC(i,k\mid j)=\frac {C(i,k)-C(i,j)C(k,j)}{\sqrt{[1-C^2(i,j)][1-C^2(k,j)]}} }[/math]

where [math]\displaystyle{ C(i,j), C(i,k) }[/math] and [math]\displaystyle{ C(j,k) }[/math] are the node correlations defined above.

The correlation influence and correlation dependency

The relative effect of the correlations [math]\displaystyle{ C(i,j) }[/math] and [math]\displaystyle{ C(j,k) }[/math] of node j on the correlation C(i,k) is given by:

[math]\displaystyle{ d(i,k\mid j)\equiv C(i,k)-PC(i,k|j) }[/math]

This avoids the trivial case were node j appears to strongly affect the correlation [math]\displaystyle{ C(i,k) }[/math] , mainly because [math]\displaystyle{ C(i,j), C(i,k) }[/math] and [math]\displaystyle{ C(j,k) }[/math] have small values. We note that this quantity can be viewed either as the correlation dependency of C(i,k) on node j (the term used here) or as the correlation influence of node j on the correlation C(i,k).

Node activity dependencies

Next, we define the total influence of node j on node i, or the dependency D(i,j) of node i on node j to be:

[math]\displaystyle{ D(i,j)=\frac {1}{N-1}\sum_{k \ne j}^{N-1} d(i,k\mid j) }[/math]

As defined,D(i,j) is a measure of the average influence of node j on the correlations C(i,k) over all nodes k not equal to j. The node activity dependencies define a dependency matrix D whose (i,j) element is the dependency of node i on node j. It is important to note that while the correlation matrix C is a symmetric matrix, the dependency matrix D is nonsymmetrical – [math]\displaystyle{ D(i,j) \ne D(j,i) }[/math] since the influence of node j on node i is not equal to the influence of node i on node j. For this reason, some of the methods used in the analyses of the correlation matrix (e.g. the PCA) have to be replaced or are less efficient. Yet there are other methods, as the ones used here, that can properly account for the non-symmetric nature of the dependency matrix.

The structure dependency networks

The path influence and distance dependency: The relative effect of node j on the directed path [math]\displaystyle{ DP(i\rightarrow k|j) }[/math] – the shortest topological path with each segment corresponds to a distance 1, between nodes i and k is given:

[math]\displaystyle{ DP(i\rightarrow k\mid j) \equiv \frac {1}{td(i \rightarrow k\mid j^+)} - \frac {1}{td(i \rightarrow k\mid j^-)} }[/math]

where [math]\displaystyle{ td(i \rightarrow k|j^+) }[/math] and [math]\displaystyle{ td(i \rightarrow k\mid j^-) }[/math] are the shortest directed topological path from node i to node k in the presence and the absence of node j respectively.

Node structural dependencies

Next, we define the total influence of node j on node i, or the dependency D(i,j) of node i on node j to be:

[math]\displaystyle{ D(i,j)=\frac {1}{N-1}\sum_{k = 1}^{N-1} DP(i\rightarrow k\mid j) }[/math]

As defined, D(i,j) is a measure of the average influence of node j on the directed paths from node i to all other nodes k. The node structural dependencies define a dependency matrix D whose (i,j) element is the dependency of node i on node j, or the influence of node j on node i. It is important to note that the dependency matrix D is nonsymmetrical – [math]\displaystyle{ D(i,j) \ne D(j,i) }[/math] since the influence of node j on node i is not equal to the influence of node i on node j.

Visualization of the dependency network

The dependency matrix is the weighted adjacency matrix, representing the fully connected network. Different algorithms can be applied to filter the fully connected network to obtain the most meaningful information, such as using a threshold approach,[1] or different pruning algorithms. A widely used method to construct informative sub-graph of a complete network is the Minimum Spanning Tree (MST).[10][11][12][13][14] Another informative sub-graph, which retains more information (in comparison to the MST) is the Planar Maximally Filtered Graph (PMFG)[15] which is used here. Both methods are based on hierarchical clustering and the resulting sub-graphs include all the N nodes in the network whose edges represent the most relevant association correlations. The MST sub-graph contains [math]\displaystyle{ (N-1) }[/math]edges with no loops while the PMFG sub-graph contains [math]\displaystyle{ 3(N-2) }[/math] edges.

See also

References

  1. ↑ 1.0 1.1 1.2 Kenett, Dror Y.; Tumminello, Michele; Madi, Asaf; Gur-Gershgoren, Gitit; Mantegna, Rosario N.; Ben-Jacob, Eshel (2010-12-20). Scalas, Enrico. ed. "Dominating Clasp of the Financial Sector Revealed by Partial Correlation Analysis of the Stock Market" (in en). PLOS ONE 5 (12): e15032. doi:10.1371/journal.pone.0015032. ISSN 1932-6203. PMID 21188140. Bibcode: 2010PLoSO...515032K. 
  2. ↑ Dror Y. Kenett, Yoash Shapira, Gitit Gur-Gershgoren, and Eshel Ben-Jacob (submitted), Index Cohesive Force analysis of the U.S. stock market, Proceedings of the 2011 International Conference on Econophysics, Kavala, Greece
  3. ↑ 3.0 3.1 Asaf Madi, Dror Y. Kenett, Sharron Bransburg-Zabary, Yifat Merbl, Francisco J. Quintana, Stefano Boccaletti, Alfred I. Tauber, Irun R. Cohen, and Eshel Ben-Jacob (2011), Analyses of antigen dependency networks unveil immune system reorganization between birth and adulthood, Chaos 21, 016109
  4. ↑ 4.0 4.1 Kenett, Yoed N.; Kenett, Dror Y.; Ben-Jacob, Eshel; Faust, Miriam (2011-08-24). Perc, Matjaz. ed. "Global and Local Features of Semantic Networks: Evidence from the Hebrew Mental Lexicon" (in en). PLOS ONE 6 (8): e23912. doi:10.1371/journal.pone.0023912. ISSN 1932-6203. PMID 21887343. Bibcode: 2011PLoSO...623912K. 
  5. ↑ Kunihiro Baba, Ritel Shibata, Masaaki Sibuya (2004), Partial correlation and conditional correlation as measures of conditional independence, Aust New Zealand J Stat 46(4): 657–774
  6. ↑ Yoash Shapira, Dror Y. Kenett, and Eshel Ben-Jacob (2009), The Index Cohesive Effect on Stock Market Correlations, Journal of Physics B. vol. 72, no. 4, pp. 657–669
  7. ↑ Kenett, Dror Y.; Shapira, Yoash; Madi, Asaf; Bransburg-Zabary, Sharron; Gur-Gershgoren, Gitit; Ben-Jacob, Eshel (2011-04-27). Scalas, Enrico. ed. "Index Cohesive Force Analysis Reveals That the US Market Became Prone to Systemic Collapses Since 2002" (in en). PLOS ONE 6 (4): e19378. doi:10.1371/journal.pone.0019378. ISSN 1932-6203. PMID 21556323. Bibcode: 2011PLoSO...619378K. 
  8. ↑ Dror Y. Kenett, Matthias Raddant, Thomas Lux, and Eshel Ben-Jacob (submitted), Evolvement of uniformity and volatility in the stressed global market, PNAS
  9. ↑ Eran Stark, Rotem Drori and Moshe Abeles (2006), Partial Cross-Correlation Analysis Resolves Ambiguity in the Encoding of Multiple Movement Features, J Neurophysiol 95: 1966–1975
  10. ↑ Rosario N. Mantegna, Hierarchical structure in Financial markets, Eur. Phys. J. B 11 (1), 193–197 (1999)
  11. ↑ Rosario N. Mantegna, Computer Physics Communications 121–122, 153–156 (1999)
  12. ↑ Guillermo J. Ortega, Rafael G. Sola and Jesus Pastor, Complex network analysis of Human ECoG data, Neuroscience Letters 447 (2-3), 129–133 (2008)[yes|permanent dead link|dead link}}]
  13. ↑ Michele Tumminello, Claudia Coronnello, Fabrizio Lillo, Salvatore Miccichè and Rrosario N. Mantegna, Spanning trees and bootstrap reliability estimations in correlation based networks [1]
  14. ↑ Douglas B. West, An Introduction to Graph Theory, edited by Prentice-Hall, Englewood Cliffs, NJ, 2001
  15. ↑ Michele Tumminello, Tomaso Aste, Tiziana Di Matteo and Rosario N. Mantegna, A tool for filtering information in complex systems, PNAS 102 (30), 10421–10426 (2005)



Retrieved from "https://handwiki.org/wiki/index.php?title=Dependency_network&oldid=3363522"