Dinatural transformation

Short description: Generalization of natural transformations

In category theory, a branch of mathematics, a dinatural transformation [math]\displaystyle{ \alpha }[/math] between two functors

[math]\displaystyle{ S,T : C^{\mathrm{op}}\times C\to D, }[/math]

written

[math]\displaystyle{ \alpha : S\ddot\to T, }[/math]

is a function that to every object [math]\displaystyle{ c }[/math] of [math]\displaystyle{ C }[/math] associates an arrow

[math]\displaystyle{ \alpha_c : S(c,c)\to T(c,c) }[/math] of [math]\displaystyle{ D }[/math]

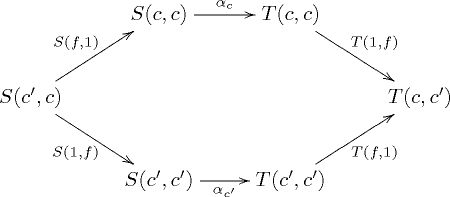
and satisfies the following coherence property: for every morphism [math]\displaystyle{ f:c\to c' }[/math] of [math]\displaystyle{ C }[/math] the diagram

commutes.

The composition of two dinatural transformations need not be dinatural.

See also

• Extranatural transformation
• Natural transformation

External links

• dinatural transformation in nLab