Directional-change intrinsic time
Directional-change intrinsic time is an event-based operator to dissect a data series into a sequence of alternating trends of defined size [math]\displaystyle{ \delta }[/math].
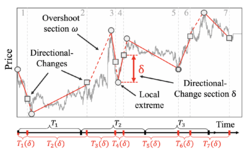
The directional-change intrinsic time operator was developed for the analysis of financial market data series. It is an alternative methodology to the concept of continuous time.[1] Directional-change intrinsic time operator dissects a data series into a set of drawups and drawdowns or up and down trends that alternate with each other. An established trend comes to an end as soon as a trend reversal is observed. A price move that extends a trend is called overshoot and leads to new price extremes.
Figure 1 provides an example of a price curve dissected by the directional change intrinsic time operator.
The frequency of directional-change intrinsic events maps (1) the volatility of price changes conditional to (2) the selected threshold [math]\displaystyle{ \delta }[/math]. The stochastic nature of the underlying process is mirrored in the non-equal number of intrinsic events observed over equal periods of physical time.
Directional-change intrinsic time operator is a noise filtering technique. It identifies regime shifts, when trend changes of a particular size occur and hides price fluctuations that are smaller than the threshold [math]\displaystyle{ \delta }[/math].
Application
The directional-change intrinsic time operator was used to analyze high frequency foreign exchange market data and has led to the discovery of a large set of scaling laws that have not been previously observed.[2] The scaling laws identify properties of the underlying data series, such as the size of the expected price overshoot after an intrinsic time event or the number of expected directional-changes within a physical time interval or price threshold. For example, a scaling relating the expected number of directional-changes [math]\displaystyle{ N(\delta) }[/math] observed over the fixed period to the size of the threshold [math]\displaystyle{ \delta }[/math]:
[math]\displaystyle{ N(\delta) = \left( \frac{\delta}{C_{N, DC}} \right)^{E_{N, DC}} }[/math],
where [math]\displaystyle{ C_{N, DC} }[/math] and [math]\displaystyle{ E_{N, DC} }[/math] are the scaling law coefficients.[3]
Other applications of the directional-change intrinsic time in finance include:
- trading strategy characterised by the annual Sharpe ratio 3.04[4]
- tools designed to monitor liquidity at multiple trend scales.[5]
The methodology can also be used for applications beyond economics and finance. It can be applied to other scientific domains and opens a new avenue of research in the area of BigData.
References
Text in this draft was copied from Petrov, Vladimir; Golub, Anton; Olsen, Richard (2019). "Instantaneous Volatility Seasonality of High-Frequency Markets in Directional-Change Intrinsic Time" (in en). Journal of Risk and Financial Management 12 (2): 54. doi:10.3390/jrfm12020054., which is available under a Creative Commons Attribution 4.0 International License.
- ↑ Guillaume, Dominique M.; Dacorogna, Michel M.; Davé, Rakhal R.; Müller, Ulrich A.; Olsen, Richard B.; Pictet, Olivier V. (1997-04-01). "From the bird's eye to the microscope: A survey of new stylized facts of the intra-daily foreign exchange markets" (in en). Finance and Stochastics 1 (2): 95–129. doi:10.1007/s007800050018. ISSN 0949-2984.
- ↑ Glattfelder, J. B.; Dupuis, A.; Olsen, R. B. (2011-04-01). "Patterns in high-frequency FX data: discovery of 12 empirical scaling laws". Quantitative Finance 11 (4): 599–614. doi:10.1080/14697688.2010.481632. ISSN 1469-7688.
- ↑ Guillaume, Dominique M.; Dacorogna, Michel M.; Davé, Rakhal R.; Müller, Ulrich A.; Olsen, Richard B.; Pictet, Olivier V. (1997-04-01). "From the bird's eye to the microscope: A survey of new stylized facts of the intra-daily foreign exchange markets" (in en). Finance and Stochastics 1 (2): 95–129. doi:10.1007/s007800050018. ISSN 0949-2984.
- ↑ Golub, Anton; Glattfelder, James; Olsen, Richard B. (2017-04-05) (in en). The Alpha Engine: Designing an Automated Trading Algorithm. Rochester, NY.
- ↑ Golub, Anton; Chliamovitch, Gregor; Dupuis, Alexandre; Chopard, Bastien (2016-01-01). "Multi-scale representation of high frequency market liquidity" (in en). Algorithmic Finance 5 (1–2): 3–19. doi:10.3233/AF-160054. ISSN 2158-5571.
 |  |
