Discrete-time beamforming

Beamforming is a signal processing technique used to spatially select propagating waves (most notably acoustic and electromagnetic waves). In order to implement beamforming on digital hardware the received signals need to be discretized. This introduces quantization error, perturbing the array pattern. For this reason, the sample rate must be generally much greater than the Nyquist rate.

Introduction

Beamforming aims to solve the problem of filtering signals coming from a certain direction as opposed to an omni-directional approach. Discrete-time beamforming is primarily of interest in the fields of seismology, acoustics, sonar and low frequency wireless communications. Antennas regularly make use of beamforming but it is mostly contained within the analog domain.

Beamforming begins with an array of sensors to detect a 4-D signal (3 physical dimensions and time). A 4-D signal [math]\displaystyle{ s(\mathbf{x},t) }[/math] exists in the spatial domain at position [math]\displaystyle{ \mathbf{x} }[/math] and at time [math]\displaystyle{ t }[/math]. The 4-D Fourier transform of the signal yields [math]\displaystyle{ S(\mathbf{k},\omega) }[/math] which exists in the wavenumber-frequency spectrum. The wavenumber vector [math]\displaystyle{ \mathbf{k} }[/math] represents the 3-D spatial frequency and [math]\displaystyle{ \omega }[/math] represents the temporal frequency. The 4-D sinusoid [math]\displaystyle{ e^{j(\omega t - \mathbf{k}' \mathbf{x})} }[/math], where [math]\displaystyle{ \mathbf{k}' }[/math] denotes the transpose of the vector [math]\displaystyle{ \mathbf{k} }[/math], can be rewritten as [math]\displaystyle{ e^{j \omega(t - \boldsymbol{\alpha}' \mathbf{x})} }[/math] where [math]\displaystyle{ \boldsymbol{\alpha} = \frac{\mathbf{k}}{\omega} }[/math] , also known as the slowness vector.

Steering the beam in a particular direction requires that all the sensors add in phase to the particular direction of interest. In order for each sensor to add in phase, each sensor will have a respective delay [math]\displaystyle{ \tau }[/math] such that [math]\displaystyle{ \boldsymbol{\tau_i} = -\boldsymbol{\alpha_o}' \mathbf{x_i} }[/math] is the delay of the ith sensor at position [math]\displaystyle{ \mathbf{x_i} }[/math] and where the direction of the slowness vector [math]\displaystyle{ \boldsymbol{\alpha_o} }[/math] is the direction of interest.

Discrete-time weighted delay-and-sum beamforming

Source:

The discrete-time beamformer output [math]\displaystyle{ bf(nT) }[/math] is formed by sampling the receiver signal [math]\displaystyle{ r_i(t) }[/math] and averaging its weighted and delayed versions.

[math]\displaystyle{ bf(nT) = \frac{1}{N} \sum_{i=0}^{N-1} w_i r_i (nT - n_iT) }[/math]

where:

• [math]\displaystyle{ N }[/math] is the number of sensors
• [math]\displaystyle{ w_i }[/math] are the weights
• [math]\displaystyle{ T }[/math] is the sampling period
• [math]\displaystyle{ n_i T }[/math] is the steering delay for the ith sensor

Setting [math]\displaystyle{ n_i T }[/math] equal to [math]\displaystyle{ -\boldsymbol{\alpha_o}' \mathbf{x_i} }[/math] would achieve the proper direction but [math]\displaystyle{ n_i }[/math] must be an integer. In most cases [math]\displaystyle{ n_i }[/math] will need to be quantized and errors will be introduced. The quantization errors can be described as [math]\displaystyle{ \Delta \tau_i = n_i T - \tau_i }[/math]. The array pattern for a desired direction given by the slowness vector [math]\displaystyle{ \alpha_o }[/math] and for a quantization error [math]\displaystyle{ \Delta \tau_i }[/math] becomes:

[math]\displaystyle{ H(\mathbf{k},\omega) = \frac{1}{N} \sum_{i=0}^{N-1} w_i e^{ -j(\mathbf{k} - \omega \boldsymbol{\alpha_0})' \mathbf{x_i}} e^{ -j \omega \Delta \tau_i } }[/math]

Interpolation

Source:

Flowchart of upsample and linear filter for discrete-time beamforming

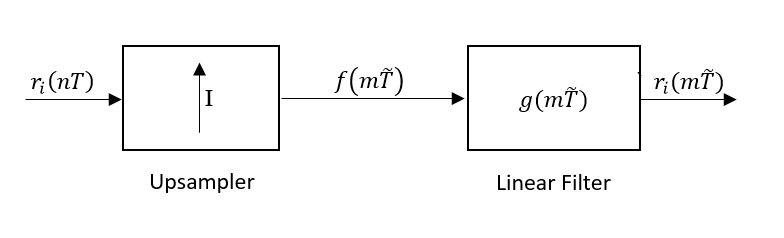
The fundamental problem of discrete weighted delay-and-sum beamforming is quantization of the steering delay. The interpolation method aims to solve this problem by upsampling the receiving signal. [math]\displaystyle{ n_i }[/math] must still be an integer but it now has a finer control. Interpolation comes at the cost of more computation. The new sample rate is denoted as [math]\displaystyle{ \tilde{T} }[/math]. The beamformer output [math]\displaystyle{ bf(n\tilde{T}) }[/math] is now

[math]\displaystyle{ bf(n\tilde{T}) = \frac{1}{N} \sum_{i=0}^{N-1} w_i \tilde{r}_i(n\tilde{T} -n_i\tilde{T}) }[/math]

The sampling period ratio [math]\displaystyle{ I = \frac{T}{\tilde{T}} }[/math] is set to an integer to minimize the increase in computations. The samples [math]\displaystyle{ \tilde{r}_i(m\tilde{T}) }[/math] are interpolated from [math]\displaystyle{ r_i(nT) }[/math] such that

[math]\displaystyle{ \tilde{r}_i(m\tilde{T}) = \sum_n r_i(nT)g((m - nI)\tilde{T}) }[/math]

After [math]\displaystyle{ bf(n\tilde{T}) }[/math] is upsampled and filtered, the beamformer output [math]\displaystyle{ bf(m\tilde{T}) }[/math] becomes:

[math]\displaystyle{ bf(m\tilde{T}) = \frac{1}{N} \sum_{i=0}^{N-1} w_i \sum_p r_i(pT) g((m- pI - n_i) \tilde{T}) }[/math]

At this point the beamformer's sample rate is greater than the highest frequency it contains.

Frequency-domain beamforming

Source:

As seen in the discrete-time domain beamforming section, the weighted delay-and-sum method is effective and compact. Unfortunately quantization errors can perturb the array pattern enough to cause complications. The interpolation technique reduces the array pattern perturbations at the cost of a higher sampling rate and more computations on digital hardware. Frequency-domain beamforming does not require a higher sampling rate which makes the method more computationally efficient.

The discrete-time frequency-domain beamformer is given by

[math]\displaystyle{ fd(nT,\omega) = \frac{1}{N} \sum_{i=0}^{N-1}w_i R_i(nT,\omega)e^ {j\omega(n-\boldsymbol{\tau}_i)} }[/math]

For linearly spaced sensor arrays [math]\displaystyle{ \boldsymbol{\tau}_i = - \frac{Mq}{Nl} i }[/math]. The discrete short-time Fourier transform of [math]\displaystyle{ r_i(nT) }[/math] is denoted by [math]\displaystyle{ R_i(nT,\omega) }[/math]. In order to be computationally efficient it is desirable to evaluate the sum in as few calculations as possible. For simplicity [math]\displaystyle{ T = 1 }[/math] moving forward. An effective method exists by considering a 1-D FFT for many values of [math]\displaystyle{ \omega }[/math]. If [math]\displaystyle{ \omega = \frac{2\pi l}{M} }[/math] for [math]\displaystyle{ 0 \le l \lt M }[/math] then [math]\displaystyle{ R_i(n,\omega)e^ {j\omega(n-\boldsymbol{\tau}_i)} }[/math] becomes:

[math]\displaystyle{ R_i \left( n, \frac{2\pi l}{M} \right) e^{j \frac{2\pi l}{M} n } = \sum_{p=0}^{M-1} r_i(n - p)v(p) e^{j \frac{2\pi l}{M} p} }[/math]

where [math]\displaystyle{ p = n-m }[/math]. Substituting the 1-D FFT into the frequency-domain beamformer:

[math]\displaystyle{ fd \left( n,\frac{2\pi l}{M} \right) = \left[ \frac{1}{N} \sum_{i=0}^{N-1} w_i R_i \left( n, \frac{2\pi l}{M} e^{j \frac{2\pi q}{N} i} \right) \right] e^{ j \frac{2\pi l}{M} n} }[/math]

The term in brackets is the 2-D DFT with the opposite sign in the exponential

[math]\displaystyle{ fd \left( n,\frac{2\pi l}{M} \right) = \frac{1}{N} \sum_{i=0}^{N-1} \sum_{p=0}^{M-1} w_i v(p) r_i(n-p) e^{j \frac{2\pi l}{M} p + j \frac{2\pi q}{N} i} }[/math]

if the 2-D sequence [math]\displaystyle{ x_n(p,i) = w_i v(p) r_i(n-p) }[/math] and [math]\displaystyle{ X_n(l,q) }[/math] is the (M X N)-point DFT of [math]\displaystyle{ x_n(p,i) }[/math] then

[math]\displaystyle{ fd \left( n,\frac{2\pi l}{M} \right) = \frac{1}{N} X_n(M-l,N-q) }[/math]

For a 1-D linear array along the horizontal direction and a desired direction:

[math]\displaystyle{ \alpha_{0x} = \frac{Mq}{NlD} }[/math]

where:

• [math]\displaystyle{ M }[/math] and [math]\displaystyle{ N }[/math] are dimensions of the DFT
• [math]\displaystyle{ D }[/math] is the sensor separation
• [math]\displaystyle{ l }[/math] is the frequency index between [math]\displaystyle{ 0 }[/math] and [math]\displaystyle{ M-1 }[/math]
• [math]\displaystyle{ q }[/math] is the steering index between [math]\displaystyle{ 0 }[/math] and [math]\displaystyle{ N-1 }[/math]

[math]\displaystyle{ l }[/math] and [math]\displaystyle{ q }[/math] can be selected to "steer the beam" towards a certain temporal frequency and spatial position