Dodecagonal antiprism
From HandWiki
| Uniform dodecagonal antiprism | |
|---|---|
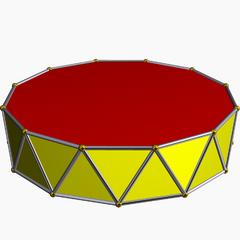
| |
| Type | Prismatic uniform polyhedron |
| Elements | F = 26, E = 48 V = 24 (χ = 2) |
| Faces by sides | 24{3}+2{12} |
| Schläfli symbol | s{2,24} sr{2,12} |
| Wythoff symbol | | 2 2 12 |
| Coxeter diagram | |
| Symmetry group | D12d, [2+,24], (2*12), order 48 |
| Rotation group | D12, [12,2]+, (12.2.2), order 24 |
| References | U77(j) |
| Dual | Dodecagonal trapezohedron |
| Properties | convex |
 Vertex figure 3.3.3.12 | |
In geometry, the dodecagonal antiprism is the tenth in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.
Antiprisms are similar to prisms except the bases are twisted relative to each other, and that the side faces are triangles, rather than quadrilaterals.
In the case of a regular 12-sided base, one usually considers the case where its copy is twisted by an angle 180°/n. Extra regularity is obtained by the line connecting the base centers being perpendicular to the base planes, making it a right antiprism. As faces, it has the two n-gonal bases and, connecting those bases, 2n isosceles triangles.
If faces are all regular, it is a semiregular polyhedron.
See also
External links
