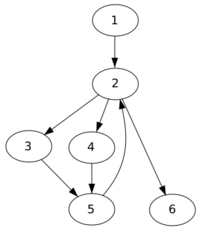
Dominator (graph theory)
| 1 | dom | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 2 | dom | 2 | 3 | 4 | 5 | 6 | |
| 3 | dom | 3 | |||||
| 4 | dom | 4 | |||||
| 5 | dom | 5 | |||||
| 6 | dom | 6 | |||||
| Corresponding domination relation: Grey nodes are not strictly dominated Red nodes are immediately dominated | |||||||
In computer science, a node d of a control-flow graph dominates a node n if every path from the entry node to n must go through d. Notationally, this is written as d dom n (or sometimes d ≫ n). By definition, every node dominates itself.
There are a number of related concepts:
- A node d strictly dominates a node n if d dominates n and d does not equal n.
- The immediate dominator or idom of a node n is the unique node that strictly dominates n but does not strictly dominate any other node that strictly dominates n. Every node, except the entry node, has an immediate dominator.[1]
- The dominance frontier of a node d is the set of all nodes ni such that d dominates an immediate predecessor of ni, but d does not strictly dominate ni. It is the set of nodes where d's dominance stops.
- A dominator tree is a tree where each node's children are those nodes it immediately dominates. The start node is the root of the tree.
History
Dominance was first introduced by Reese T. Prosser in a 1959 paper on analysis of flow diagrams.[2] Prosser did not present an algorithm for computing dominance, which had to wait ten years for Edward S. Lowry and C. W. Medlock.[3] Ron Cytron et al. rekindled interest in dominance in 1989 when they applied it to the problem of efficiently computing the placement of φ functions, which are used in static single assignment form.[4]
Applications
Dominators, and dominance frontiers particularly, have applications in compilers for computing static single assignment form. A number of compiler optimizations can also benefit from dominators. The flow graph in this case comprises basic blocks.
Automatic parallelization benefits from postdominance frontiers. This is an efficient method of computing control dependence, which is critical to the analysis.
Memory usage analysis can benefit from the dominator tree to easily find leaks and identify high memory usage.[5]
In hardware systems, dominators are used for computing signal probabilities for test generation, estimating switching activities for power and noise analysis, and selecting cut points in equivalence checking.[6] In software systems, they are used for reducing the size of the test set in structural testing techniques such as statement and branch coverage.[7]
Algorithms
Let [math]\displaystyle{ n_0 }[/math] be the source node on the Control-flow graph. The dominators of a node [math]\displaystyle{ n }[/math] are given by the maximal solution to the following data-flow equations:
- [math]\displaystyle{ \operatorname{Dom}(n) = \begin{cases} \left \{ n \right \} & \mbox{ if } n = n_0 \\ \left \{ n \right \} \cup \left ( \bigcap_{p \in \text{preds}(n)}^{} \operatorname{Dom}(p) \right ) & \mbox{ if } n \neq n_0 \end{cases} }[/math]
The dominator of the start node is the start node itself. The set of dominators for any other node [math]\displaystyle{ n }[/math] is the intersection of the set of dominators for all predecessors [math]\displaystyle{ p }[/math] of [math]\displaystyle{ n }[/math]. The node [math]\displaystyle{ n }[/math] is also in the set of dominators for [math]\displaystyle{ n }[/math].
An algorithm for the direct solution is:
// dominator of the start node is the start itself
Dom(n0) = {n0}
// for all other nodes, set all nodes as the dominators
for each n in N - {n0}
Dom(n) = N;
// iteratively eliminate nodes that are not dominators
while changes in any Dom(n)
for each n in N - {n0}:
Dom(n) = {n} union with intersection over Dom(p) for all p in pred(n)
The direct solution is quadratic in the number of nodes, or O(n2). Lengauer and Tarjan developed an algorithm which is almost linear,[1] and in practice, except for a few artificial graphs, the algorithm and a simplified version of it are as fast or faster than any other known algorithm for graphs of all sizes and its advantage increases with graph size.[8]
Keith D. Cooper, Timothy J. Harvey, and Ken Kennedy of Rice University describe an algorithm that essentially solves the above data flow equations but uses well engineered data structures to improve performance.[9]
Postdominance
Analogous to the definition of dominance above, a node z is said to post-dominate a node n if all paths to the exit node of the graph starting at n must go through z. Similarly, the immediate post-dominator of a node n is the postdominator of n that doesn't strictly postdominate any other strict postdominators of n.
See also
References
- ↑ 1.0 1.1 Lengauer, Thomas; Tarjan, Robert Endre (July 1979). "A fast algorithm for finding dominators in a flowgraph". ACM Transactions on Programming Languages and Systems 1 (1): 121–141. doi:10.1145/357062.357071.
- ↑ Prosser, Reese T. (1959). "Applications of Boolean matrices to the analysis of flow diagrams". AFIPS Joint Computer Conferences: Papers Presented at the December 1–3, 1959, Eastern Joint IRE-AIEE-ACM Computer Conference. IRE-AIEE-ACM '59 (Eastern): 133–138. doi:10.1145/1460299.1460314. http://portal.acm.org/ft_gateway.cfm?id=1460314&type=pdf&coll=GUIDE&dl=GUIDE&CFID=79528182&CFTOKEN=33765747.
- ↑ Lowry, Edward S.; Medlock, Cleburne W. (January 1969). "Object code optimization". Communications of the ACM 12 (1): 13–22. doi:10.1145/362835.362838.
- ↑ Cytron, Ron; Ferrante, Jeanne; Rosen, Barry K.; Wegman, Mark N.; Zadeck, F. Kenneth (1989). "An efficient method of computing static single assignment form". Proceedings of the 16th ACM SIGPLAN-SIGACT symposium on Principles of programming languages - POPL '89. POPL ’89. pp. 25–35. doi:10.1145/75277.75280. ISBN 0897912942. http://portal.acm.org/citation.cfm?doid=75277.75280.
- ↑ "Dominator Tree". SAP AG and IBM Corporation. 2012. http://help.eclipse.org/juno/index.jsp?topic=%2Forg.eclipse.mat.ui.help%2Fconcepts%2Fdominatortree.html.
- ↑ Teslenko, Maxim; Dubrova, Elena (2005). "An Efficient Algorithm for Finding Double-Vertex Dominators in Circuit Graphs". Design, Automation and Test in Europe. Date '05. pp. 406–411. doi:10.1109/DATE.2005.53. ISBN 9780769522883. http://dl.acm.org/citation.cfm?id=1049138.
- ↑ Dubrova, Elena (2005). "Structural Testing Based on Minimum Kernels". Design, Automation and Test in Europe. Date '05. pp. 1168–1173. doi:10.1109/DATE.2005.284. ISBN 9780769522883. http://dl.acm.org/citation.cfm?id=1049294.
- ↑ "Finding Dominators in Practice". 2006. http://jgaa.info/accepted/2006/GeorgiadisTarjanWerneck2006.10.1.pdf.
- ↑ "A Simple, Fast Dominance Algorithm". 2001. http://www.hipersoft.rice.edu/grads/publications/dom14.pdf.
External links
 |