Doubly logarithmic tree
From HandWiki
Short description: Concept in computer science
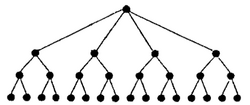
In computer science, a doubly logarithmic tree is a tree where each internal node of height 1, the tree layer above the leaves, has two children, and each internal node of height [math]\displaystyle{ h \gt 1 }[/math] has [math]\displaystyle{ 2^{2^{h-2}} }[/math] children. Each child of the root contains [math]\displaystyle{ \sqrt{n} }[/math] leaves.[1] The number of children at a node from each leaf to root is 0,2,2,4,16, 256, 65536, ... (sequence A001146 in the OEIS)
A similar tree called a k-merger is used in Prokop et al.'s cache oblivious Funnelsort to merge elements.[2]
References
- ↑ Berkman, Omer; Schieber, Baruch; Vishkin, Uzi (1993), "Optimal doubly logarithmic parallel algorithms based on finding all nearest smaller values", Journal of Algorithms 14 (3): 344–370, doi:10.1006/jagm.1993.1018
- ↑ Harald Prokop. Cache-Oblivious Algorithms. Masters thesis, MIT. 1999.
Further reading
- M. Frigo, C.E. Leiserson, H. Prokop, and S. Ramachandran. Cache-oblivious algorithms. In Proceedings of the 40th IEEE Symposium on Foundations of Computer Science (FOCS 99), p. 285-297. 1999. Extended abstract at IEEE, at Citeseer.
- Demaine, Erik. Review of the Cache-Oblivious Sorting. Notes for MIT Computer Science 6.897: Advanced Data Structures.
 |