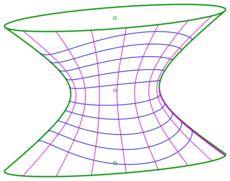
Dupin's theorem

Orthogonal surfaces through a point

Two planes (purple, blue) as members of a threefold orthogonal system intersect a cylinder at curvature lines (blue circle, purble line)

In differential geometry Dupin's theorem, named after the French mathematician Charles Dupin, is the statement:

• The intersection curve of any pair of surfaces of different pencils of a threefold orthogonal system is a curvature line.

A threefold orthogonal system of surfaces consists of three pencils of surfaces such that any pair of surfaces out of different pencils intersect orthogonally.

The most simple example of a threefold orthogonal system consists of the coordinate planes and their parallels. But this example is of no interest, because a plane has no curvature lines.

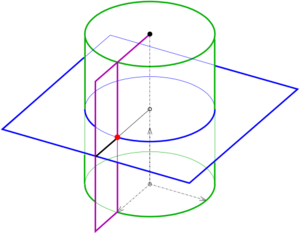
A simple example with at least one pencil of curved surfaces: 1) all right circular cylinders with the z-axis as axis, 2) all planes, which contain the z-axis, 3) all horizontal planes (see diagram).

A curvature line is a curve on a surface, which has at any point the direction of a principal curvature (maximal or minimal curvature). The set of curvature lines of a right circular cylinder consists of the set of circles (maximal curvature) and the lines (minimal curvature). A plane has no curvature lines, because any normal curvature is zero. Hence, only the curvature lines of the cylinder are of interest: A horizontal plane intersects a cylinder at a circle and a vertical plane has lines with the cylinder in common.

The idea of threefold orthogonal systems can be seen as a generalization of orthogonal trajectories. Special examples are systems of confocal conic sections.

Application

Dupin's theorem is a tool for determining the curvature lines of a surface by intersection with suitable surfaces (see examples), without time-consuming calculation of derivatives and principal curvatures. The next example shows, that the embedding of a surface into a threefold orthogonal system is not unique.

Examples

Right circular cone

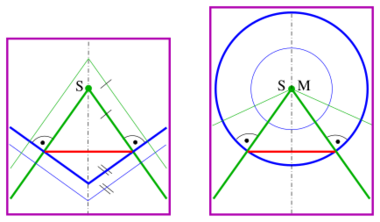
Given: A right circular cone, green in the diagram.
Wanted: The curvature lines.

orthogonal system (purple, green, blue) of surfaces for the cone (green), curvature lines: green, red

1. pencil: Shifting the given cone C with apex S along its axis generates a pencil of cones (green).
2. pencil: Cones with apexes on the axis of the given cone such that the lines are orthogonal to the lines of the given cone (blue).
3. pencil: Planes through the cone's axis (purple).

These three pencils of surfaces are an orthogonal system of surfaces. The blue cones intersect the given cone C at a circle (red). The purple planes intersect at the lines of cone C (green).

Alternative with spheres

The points of the space can be described by the spherical coordinates [math]\displaystyle{ (r,\varphi,\theta) }[/math]. It is set S=M=origin.

1. pencil: Cones with point S as apex and their axes are the axis of the given cone C (green): [math]\displaystyle{ (r,\varphi,\theta_0) }[/math].
2. pencil: Spheres centered at M=S (blue): [math]\displaystyle{ (r_0,\varphi,\theta) }[/math]
3. pencil: Planes through the axis of cone C (purple): [math]\displaystyle{ (r,\varphi_0,\theta) }[/math].

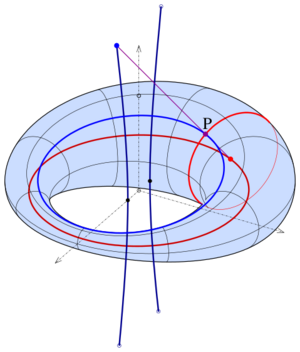
Torus

Orthogonal system (purple, green, blue) of surfaces for a torus (green)
Curvature lines: green, red

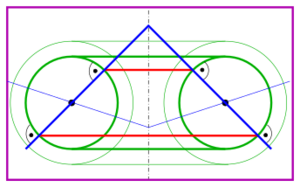
1. pencil: Tori with the same directrix (green).
2. pencil: Cones containing the directrix circle of the torus with apexes on the axis of the torus (blue).
3. pencil: Planes containing the axis of the given torus (purple).

The blue cones intersect the torus at horizontal circles (red). The purple planes intersect at vertical circles (green).

The curvature lines of a torus generate a net of orthogonal circles.

A torus contains more circles: the Villarceau circles, which are not curvature lines.

Surface of revolution

Orthogonal system for a surface of revolution (green)

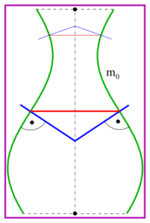
Usually a surface of revolution is determined by a generating plane curve (meridian) [math]\displaystyle{ m_0 }[/math]. Rotating [math]\displaystyle{ m_0 }[/math] around the axis generates the surface of revolution. The method used for a cone and a torus can be extended to a surface of revolution:

1. pencil: Parallel surfaces to the given surface of revolution.
2. pencil: Cones with apices on the axis of revolution with generators orthogonal to the given surface (blue).
3. pencil: Planes containing the axis of revolution (purple).

The cones intersect the surface of revolution at circles (red). The purple planes intersect at meridians (green). Hence:

• The curvature lines of a surface of revolution are the horizontal circles and the meridians.

Confocal quadrics

Ellipsoid with curvature lines

Hyperboloid with curvature lines

The article confocal conic sections deals with confocal quadrics, too. They are a prominent example of a non trivial orthogonal system of surfaces. Dupin's theorem shows that

the curvature lines of any of the quadrics can be seen as the intersection curves with quadrics out of the other pencils (see diagrams).

Confocal quadrics are never rotational quadrics, so the result on surfaces of revolution (above) cannot be applied. The curvature lines are i.g. curves of degree 4. (Curvature lines of rotational quadrics are always conic sections !)

Ellipsoid (see diagram)

Semi-axes: [math]\displaystyle{ \;a=1, \; b=0.8, \; c=0.6\; }[/math].
The curvature lines are sections with one (blue) and two (purple) sheeted hyperboloids. The red points are umbilic points.

Hyperboloid of one sheet (see diagram)

Semi-axes: [math]\displaystyle{ \;a=0.67, \; b=0.3 , \; c=0.44\; }[/math].
The curvature lines are intersections with ellipsoids (blue) and hyperboloids of two sheets (purple).

Dupin cyclides

Ring cyclide with its focal conics (dark red: ellipse, dark blue: hyperbola). Purple: surface normal and common line of the two cones at point P

A Dupin cyclide and its parallels are determined by a pair of focal conic sections. The diagram shows a ring cyclide together with its focal conic sections (ellipse: dark red, hyperbola: dark blue). The cyclide can be seen as a member of an orthogonal system of surfaces:

1. pencil: parallel surfaces of the cyclide.
2. pencil: right circular cones through the ellipse (their apexes are on the hyperbola)
3. pencil: right circular cones through the hyperbola (their apexes are on the ellipse)

The special feature of a cyclide is the property:

The curvature lines of a Dupin cyclide are circles.

Proof of Dupin's theorem

Any point of consideration is contained in exactly one surface of any pencil of the orthogonal system. The three parameters [math]\displaystyle{ u,v,w }[/math] describing these three surfaces can be considered as new coordinates. Hence any point can be represented by:

[math]\displaystyle{ x=x(u,v,w) }[/math]

[math]\displaystyle{ y=y(u,v,w) }[/math]

[math]\displaystyle{ z=z(u,v,w)\quad }[/math] or shortly: [math]\displaystyle{ \quad \vec x=\vec x(u,v,w)\; . }[/math]

For the example (cylinder) in the lead the new coordinates are the radius [math]\displaystyle{ r }[/math] of the actual cylinder, angle [math]\displaystyle{ \varphi }[/math] between the vertical plane and the x-axis and [math]\displaystyle{ \zeta }[/math] the height of the horizontal plane. Hence, [math]\displaystyle{ r,\varphi,\zeta }[/math] can be considered as the cylinder coordinates of the point of consideration.

The condition "the surfaces intersect orthogonally" at point [math]\displaystyle{ \vec x(u,v,w) }[/math] means, the surface normals [math]\displaystyle{ \; \vec x_u\times \vec x_v,\; \vec x_v\times \vec x_w, \;\vec x_w\times \vec x_u }[/math] are pairwise orthogonal. This is true, if

[math]\displaystyle{ \vec x_u,\;\vec x_v,\; \vec x_w\quad }[/math] are pairwise orthogonal. This property can be checked with help of Lagrange's identity.

Hence

(1)[math]\displaystyle{ \quad \vec x_u\cdot \vec x_v=0,\quad \vec x_v\cdot \vec x_w=0, \quad\vec x_w\cdot \vec x_u=0\; . }[/math]

Deriving these equations for the variable, which is not contained in the equation, one gets

[math]\displaystyle{ \vec x_{uw}\cdot\vec x_v+\vec x_u\cdot\vec x_{vw}=0\; , }[/math]

[math]\displaystyle{ \vec x_{uv}\cdot\vec x_w+\vec x_v\cdot\vec x_{uw}=0\; , }[/math]

[math]\displaystyle{ \vec x_{vw}\cdot\vec x_u+\vec x_w\cdot\vec x_{vw}=0\; . }[/math]

Solving this linear system for the three appearing scalar products yields:

(2)[math]\displaystyle{ \quad \vec x_{uv}\cdot \vec x_w=0,\quad \vec x_{vw}\cdot \vec x_u=0, \quad\vec x_{uw}\cdot \vec x_v=0\; . }[/math]

From (1) and (2): The three vectors [math]\displaystyle{ \vec x_u,\vec x_v,\vec x_{uv} }[/math] are orthogonal to vector [math]\displaystyle{ \vec x_w }[/math] and hence are linear dependent (are contained in a common plane), which can be expressed by:

(3)[math]\displaystyle{ \quad \det(\vec x_{uv},\vec x_u,\vec x_v)=0\; . }[/math]

From equation (1) one gets [math]\displaystyle{ F=0 }[/math] (coefficient of the first fundamental form) and
from equation (3): [math]\displaystyle{ M=0 }[/math] (coefficient of the second fundamental form) of the surface [math]\displaystyle{ \vec x = \vec x(u,v,w_0) }[/math].

Consequence: The parameter curves are curvature lines.

The analogous result for the other two surfaces through point [math]\displaystyle{ \vec x(u_0,v_0,w_0) }[/math] is true, too.

References

• H.S.M. Coxeter: Introduction to geometry, Wiley, 1961, pp. 11, 258.
• Ch. Dupin: Développements de géométrie, Paris 1813.
• F. Klein: Vorlesungen über Höhere Geometrie, Springer-Verlag, 2013, ISBN:3642886744, p. 9.
• Ludwig Schläfli: Über die allgemeinste Flächenschar zweiten Grades, die mit irgend zwei anderen Flächenscharen ein orthogonales System bildet, in L. Schläfli: Gesammelte mathematische Abhandlungen p. 163, Springer-Verlag, 2013, ISBN:3034841167.
• J. Weingarten: Über die Bedingung, unter welcher eine Flächenfamilie einem orthogonalen Flächensystem angehört., Journal für die reine und angewandte Mathematik, Band 1877, Heft 83, pp. 1–12, ISSN (Online) 1435–5345, ISSN (Print) 0075–4102.
• T. J. Willmore: An Introduction to Differential Geometry, Courier Corporation, 2013, ISBN:0486282104, p. 295.