Earth:Contour advection
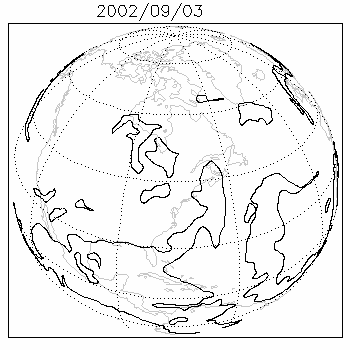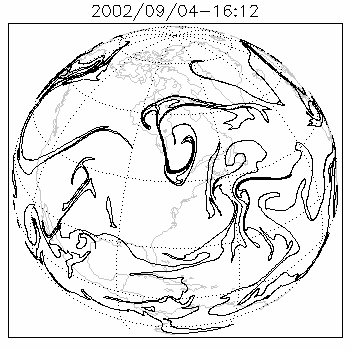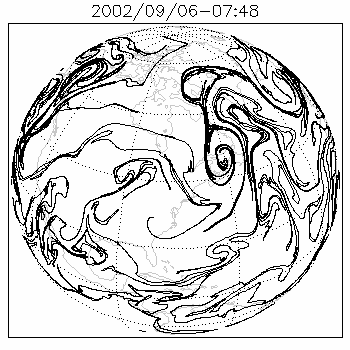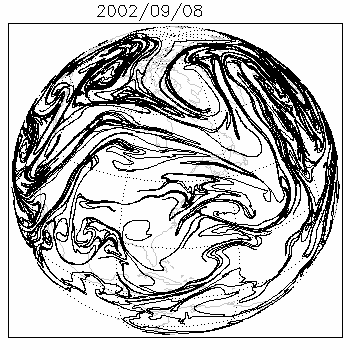
Contour advection is a Lagrangian method of simulating the evolution of one or more contours or isolines of a tracer as it is stirred by a moving fluid. Consider a blob of dye injected into a river or stream: to first order it could be modelled by tracking only the motion of its outlines. It is an excellent method for studying chaotic mixing: even when advected by smooth or finitely-resolved velocity fields, through a continuous process of stretching and folding, these contours often develop into intricate fractals. The tracer is typically passive as in [1] but may also be active as in,[2] representing a dynamical property of the fluid such as vorticity. At present, advection of contours is limited to two dimensions, but generalizations to three dimensions are possible.
Method
First we need a set of points that accurately define the contour. These points are advected forward using a trajectory integration technique. To maintain its integrity, points must be added to or removed from the curve at regular intervals based on some criterion or metric. The most obvious criterion is to maintain the distance between adjacent points within a certain interval. A better method is to use curvature since fewer points are required for the same level of precision. The curvature of a two-dimensional, Cartesian curve is given as:
- [math]\displaystyle{ \frac{1}{r} = \sqrt{\left ( \frac{\mathrm d^2 x}{\mathrm d s^2}\right )^2 + \left ( \frac{\mathrm d^2 y}{\mathrm d s^2} \right )^2} }[/math]
where [math]\displaystyle{ r }[/math] is the radius of curvature and [math]\displaystyle{ s }[/math] is the path. We need to keep the fraction of arc traced out between two adjacent points, [math]\displaystyle{ r \Delta s }[/math], where [math]\displaystyle{ \Delta s }[/math] is the path difference between them, roughly constant
In,[3] cubic spline fitting is used both to calculate the curvature and interpolate new points into the contour. The spline, which is fitted parametrically, returns a set of second-order derivatives.
Surgery
A powerful refinement to the technique involves cutting out filaments that have become too narrow to be significant. If the distance method of adding/removing points is used, then it is relatively straight forward to check the distances between all combinations of points. If a distance between non-adjacent points is too small, then the two points are separated from their neighbours, joined together and their neighbours joined also. Points may then be removed if necessary. Once we allow surgery, we allow multiply connected domains inside the same contour. A piece of the contour only one point in length would be removed from the simulation. The most challenging part of the exercise is keeping track of all the points in order to reduce the number of distance calculations---see nearest neighbour search. If the curvature method is used, then it may be difficult to recognize when two sections of the contour are close enough to apply the surgery because of differing spacing in strongly curved versus relatively straight sections.[2]
Validation
Advected contours, e.g. of trace gases (such as ozone) in the stratosphere, can be validated with satellite remote sensing instruments using a method called isoline retrieval. [3]
External links
- ctraj: A library for Lagrangian advection simulations.
References
- ↑ D. W. Waugh; R. A. Plumb (1994). "Contour advection with surgery: a technique for investigating the fine scale structure in tracer transport". Journal of the Atmospheric Sciences 51 (4): 415–422. doi:10.1175/1520-0469(1994)051<0530:CAWSAT>2.0.CO;2.
- ↑ 2.0 2.1 D. G. Dritschel (1988). "Contour surgery: A topological reconnection scheme". Journal of Computational Physics 77: 240–266. doi:10.1016/0021-9991(88)90165-9.
- ↑ 3.0 3.1 Peter Mills (2009). "Isoline retrieval: An optimal method for validation of advected contours". Computers & Geosciences 35 (11): 2020–2031. doi:10.1016/j.cageo.2008.12.015. http://peteysoft.users.sourceforge.net/Mills2009.pdf.
 |  |
