Earth:Hypsometric curve
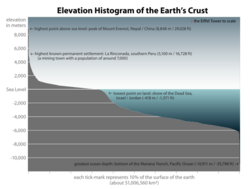
A hypsometric curve is a histogram or cumulative distribution function of elevations in a geographical area. Differences in hypsometric curves between landscapes arise because the geomorphic processes that shape the landscape may be different.
When drawn as a 2-dimensional histogram, a hypsometric curve displays the elevation (y) on the vertical, y-axis and area above the corresponding elevation (x) on the horizontal or x-axis. The curve can also be shown in non-dimensional or standardized form by scaling elevation and area by the maximum values. The non-dimensional hypsometric curve provides an hydrologist or a geomorphologist with a way to assess the similarity of watersheds — and is one of several characteristics used for doing so. The hypsometric integral is a summary measure of the shape of the hypsometric curve.
In the original paper on this topic, Arthur Strahler proposed a curve containing three parameters to fit different hypsometric relations:[1]
- ,
where a, d and z are fitting parameters. Subsequent research using two-dimensional landscape evolution models has called the general applicability of this fit into question,[2] as well as the capability of the hypsometric curve to deal with scale-dependent effects.
References
- ↑ Strahler, Arthur N. (1952). "Hypsometric (area-altitude) analysis of erosional topography". Bulletin of the Geological Society of America 63 (11): 1117–1142. doi:10.1130/0016-7606(1952)63[1117:HAAOET2.0.CO;2].
- ↑ Willgoose, G.; Hancock, G. (1998). "Revisiting the hypsometric curve as an indicator of form and process in transport‐limited catchment". Earth Surface Processes and Landforms 23 (7): 611–623. doi:10.1002/(SICI)1096-9837(199807)23:7<611::AID-ESP872>3.0.CO;2-Y.
