Earth:Moment distance index

The moment distance index (MDI) is a shape-based metric or shape index that can be used to analyze spectral reflectance curves and waveform LiDAR, proposed by Salas and Henebry in 2014. In the case of spectral data, the shape of the reflectance curve should unmask fine points of the spectra usually not considered by existing band-specific indices. It has been used to identify spectral regions for chlorophyll and carotenoids, detect greenhouses using WorldView-2, Landsat, and Sentinel-2 satellite data, identify greenhouse crops, compute canopy heights, estimate green vegetation fraction, and optimize Fourier-transform infrared (FTIR) scans for soil spectroscopy.

Various approaches have been devised to analyze medium and fine spectral resolution data and maximize their use to extract specific information for vegetation biophysical and biochemical properties. Combinations of spectral bands, called indices, have been used to diminish the effects of soil background and/or atmospheric conditions while highlighting specific spectral features associated with plant or canopy properties. Vegetation indices (VIs) use the concept of band ratio and differences or weighted linear combinations to take advantage of the visible and NIR bands, two important spectral bands for vegetation studies, in measuring the photosynthetic activity of the plant and explore vegetation dynamics. There is an extensive list of such indices, including the normalized difference vegetation index (NDVI), ratio-based indices such as the modified simplerRatio, soil-distance-based indices such as the modified soil adjusted vegetation index (MSAVI), and many others. Whereas most indices incorporate two-band or three-band relations – slope-based, distance-based on soil line or optimized (slope-based and distance-based concepts combined) – no approach deals with the raw shape of the spectral curve. MDI, however, investigates the shape of the reflectance curve using multiple spectral bands not considered by other indices, which could carry additional spectral information useful for vegetation monitoring.

A full-waveform Light Detection And Ranging (LiDAR) system has the ability to record many returns per emitted pulse, as a function of time, to reveal the vertical structure of the illuminated object, showing position of the individual targets, and finer details of the signature of intercepted surfaces or the proportion of the canopy complexity. Information associated with the illuminated object can be decoded from the generated backscattered waveform, as key features of the waveform such as the shape, area, and power are directly related to the geometry of the illuminated object. The richness of the LiDAR waveform holds a promise to address the challenge of characterizing in detail the geometric and reflection characteristics of vegetation structure, e.g., the vertical canopy volume distribution. MDI utilizes the raw waveform and place importance on its shape and its return power. MDI departs from the usual Gaussian modeling in detecting peaks (canopy and ground) for example in canopy height estimation and focus more on the full geometry (raw shape) and radiometry (raw power) of the LiDAR waveform to retain richness of the data.

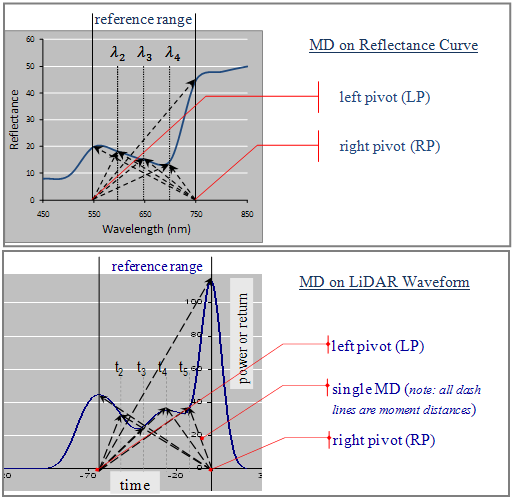
The moment distance is a matrix of distances computed from two reference locations (pivots) to each spectral or waveform point within the specified range.

Assume that a curve (reflectance or absorption curve or backscattered waveform) is displayed in Cartesian coordinates with the abscissa displaying the wavelength λ or time lapse t and the ordinate displaying the reflectance ρ or the backscattered power p. Let the subscript LP denote the left pivot (located in a shorter wavelength for the spectral curve and earlier temporal reference point for the waveform) and subscript RP denote the right pivot (located in a longer wavelength for the spectral curve and later temporal reference point for the waveform). Let λ_LP and λ_RP be the wavelength locations observed at the left and right pivots for a reflectance data, respectively, where left (right) indicates a shorter (longer) wavelength. Let t_LP and t_RP be the time value observed at the left and right pivots for a waveform data, respectively, where left (right) indicates an earlier (later) time. The proposed MD approach can be described in a set of equations.

Moment distance index (MDI) schematic diagram for spectral reflectance curve (top) and LiDAR waveform (bottom). Note the number of points between pivots can vary.

For spectral data, the index is given as:

[math]\displaystyle{ MDI = MD_{RP} - MD_{LP} }[/math]

[math]\displaystyle{ MD_{RP} = \textstyle \sum_{i=\lambda_{RP}}^{\lambda_{LP}} \displaystyle(\rho_i^2+ ({\lambda_{RP}}-i)^2)^{0.5} }[/math]

[math]\displaystyle{ MD_{LP} = \textstyle \sum_{i=\lambda_{LP}}^{\lambda_{RP}} \displaystyle(\rho_i^2+ (i-{\lambda_{LP}})^2)^{0.5} }[/math]

where [math]\displaystyle{ MDI_{RP} }[/math]is the moment distance from the right pivot, [math]\displaystyle{ MDI_{LP} }[/math]is the moment distance from the left pivot, [math]\displaystyle{ {\lambda_{LP}} }[/math]is the wavelength location at left pivot, [math]\displaystyle{ {\lambda_{RP}} }[/math]is the wavelength location at right pivot, [math]\displaystyle{ \rho_i }[/math]is the spectral reflectance at a given wavelength, and [math]\displaystyle{ i }[/math] is successive wavelength location.

For waveform LiDAR data, the index is given as:

[math]\displaystyle{ MDI = MD_{LP} - MD_{RP} }[/math]

[math]\displaystyle{ MD_{RP} = \textstyle \sum_{i=t_{RP}}^{t_{LP}} \displaystyle(\rho_i^2+ ({t_{RP}}-i)^2)^{0.5} }[/math]

[math]\displaystyle{ MD_{LP} = \textstyle \sum_{i=t_{LP}}^{t_{RP}} \displaystyle(\rho_i^2+ (i-{t_{LP}})^2)^{0.5} }[/math]

where the moment distance from the left pivot (MD_LP) is the sum of the hypotenuses constructed from the left pivot to the power at successively later times (index [math]\displaystyle{ i }[/math] from t_LP to t_RP): one base of each triangle is difference from the left pivot ([math]\displaystyle{ i }[/math] − t_LP) along the abscissa and the other base is simply the backscattered power at [math]\displaystyle{ i }[/math]. Similarly, the moment distance from the right pivot (MD_RP) is the sum of the hypotenuses constructed from the right pivot to the power at successively earlier times (index [math]\displaystyle{ i }[/math] from t_RP to t_LP): one base of each triangle is the difference from the right pivot (t_RP − [math]\displaystyle{ i }[/math]) along the abscissa and the other base is simply the backscattered power at [math]\displaystyle{ i }[/math].

MDI is an unbounded metric. It increases or decreases as a nontrivial function of the number of spectral bands or bins considered and the shape of the spectrum or waveform that spans those contiguous bands or bins. The number of bands or bins is a function of the spectral resolution of the imaging spectrometer or the temporal resolution of the LiDAR (digitization rate) and the length of the reference range (i.e., full extent or subsets of the curve) being analyzed.