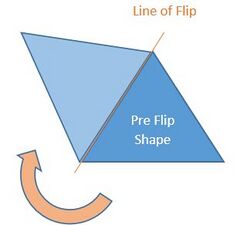
Edge tessellation
A tessellation, also known as a tiling, is a set of shapes that must cover the entire plane without the shapes overlapping. This repeating shape must cover every part of the plane without overlapping.[1] An edge tessellation, is a special type of tessellation that is created by flipping or reflecting the shape over an edge.[1] This can be also be called "folding" tessellation.
Euclidean plane
In the Euclidean plane there is a limited number of ways to create an edge tessellation. This is defined by the type of triangle and the rotations of the given triangles. The triangles that can be used are equilateral, isosceles, right triangles, and in particular 60°-right triangles. If an edge tessellation is not any of the triangles listed, then it can also be a generated by four non-obtuse polygons such as a rectangle, 120-rhombus, 60-90-120 kite, and a regular hexagon.[1]
Tessellations can happen not only in the traditional Euclidean plane, but also in various non-Euclidean planes.
Non-Euclidean plane
Hyperbolic
Hyperbolic geometry is defined by axioms and postulates. The Hyperbolic Parallel Postulate and the Asymptotically Parallel Postulates help define edge tessellations in hyperbolic geometry. The Hyperbolic Parallel Postulate states that given a line with a point parallel to the given line there are infinitely many lines connecting the point to the line. There are two types of parallelism that exists in hyperbolic geometry: asymptotically parallel and ultra/hyper parallel.[2]
The Asymptotically Parallel Postulate states that when one line moves towards zero and in the opposite direction, the other line is unbounded.[2] This allows us to see that eventually it will become impossible to continue folding edge tessellations, as we run out of possible areas to fold.
Ultra-parallel (hyper-parallel) – These lines have a common perpendicular with a given distance separating them that is considered unbounded as they move away from each other.[2]
Spherical
To fold in spherical geometry, we must assume that two points do not make a line, and that there are no parallel lines. If we assume that, then we can fold toward the point of intersection. The area in spherical geometry can be related to the area in hyperbolic geometry.
Applications of edge tessellations
Stamp folding puzzles were created based on the edge tessellation concept.[1] The constraints of folding puzzles is to fold designated shapes within the given confines of the paper. When folding the paper, there cannot be any overlaps and the shape folded must not allow gaps between the folds. It is allowed to tuck packets of paper between other leaves of the paper.
Theorems
1. A polygon that is created by edge tessellations is of one of the following types:
- Rectangle
- An equilateral triangle
- 60-right triangle
- Isosceles right triangle
- 120-isosceles triangle
- 120-rhombus
- 60-90-120 kite
- Regular hexagon
2. The edge tessellations that work well stamp folding are the four non-obtuse polygons indicated in Theorem 1.[1]
Citations