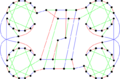
Ellingham–Horton graph
| Ellingham–Horton graphs | |
|---|---|
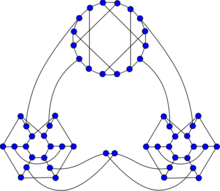 The Ellingham–Horton 54-graph. | |
| Named after | Joseph Horton and Mark Ellingham |
| Vertices | 54 (54-graph) 78 (78-graph) |
| Edges | 81 (54-graph) 117 (78-graph) |
| Radius | 9 (54-graph) 7 (78-graph) |
| Diameter | 10 (54-graph) 13 (78-graph) |
| Girth | 6 (both) |
| Automorphisms | 32 (54-graph) 16 (78-graph) |
| Chromatic number | 2 (both) |
| Chromatic index | 3 (both) |
| Book thickness | 3 (both) |
| Queue number | 2 (both) |
| Properties | Cubic (both) Bipartite (both) Regular (both) |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Ellingham–Horton graphs are two 3-regular graphs on 54 and 78 vertices: the Ellingham–Horton 54-graph and the Ellingham–Horton 78-graph.[1] They are named after Joseph D. Horton and Mark N. Ellingham, their discoverers. These two graphs provide counterexamples to the conjecture of W. T. Tutte that every cubic 3-connected bipartite graph is Hamiltonian.[2] The book thickness of the Ellingham-Horton 54-graph and the Ellingham-Horton 78-graph is 3 and the queue numbers 2.[3]
The first counterexample to the Tutte conjecture was the Horton graph, published by (Bondy Murty).[4] After the Horton graph, a number of smaller counterexamples to the Tutte conjecture were found. Among them are a 92-vertex graph by (Horton 1982),[5] a 78-vertex graph by (Owens 1983),[6] and the two Ellingham–Horton graphs.
The first Ellingham–Horton graph was published by (Ellingham 1981) and is of order 78.[7] At that time it was the smallest known counterexample to the Tutte conjecture. The second Ellingham–Horton graph was published by (Ellingham Horton) and is of order 54.[8] In 1989, Georges' graph, the smallest currently-known Non-Hamiltonian 3-connected cubic bipartite graph was discovered, containing 50 vertices.[9]
Gallery
The chromatic number of the Ellingham–Horton 54-graph is 2.
The chromatic number of the Ellingham–Horton 78-graph is 2.
References
- ↑ Weisstein, Eric W.. "Tutte Conjecture". http://mathworld.wolfram.com/TutteConjecture.html.
- ↑ Tutte, W. T. (1971), "On the 2-factors of bicubic graphs", Discrete Mathematics 1 (2): 203–208, doi:10.1016/0012-365X(71)90027-6.
- ↑ Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, Universität Tübingen, 2018
- ↑ Bondy, J. A.; Murty, U. S. R. (1976), Graph Theory with Applications, New York: North Holland, p. 240, ISBN 0-444-19451-7, https://archive.org/details/graphtheorywitha0000bond/page/240
- ↑ Horton, J. D. (1982), "On two-factors of bipartite regular graphs", Discrete Mathematics 41 (1): 35–41, doi:10.1016/0012-365X(82)90079-6.
- ↑ Owens, P. J. (1983), "Bipartite cubic graphs and a shortness exponent", Discrete Mathematics 44 (3): 327–330, doi:10.1016/0012-365X(83)90201-7.
- ↑ Ellingham, M. N. (1981), Non-Hamiltonian 3-connected cubic partite graphs, Research Report 28, Melbourne: Dept. of Math., Univ. Melbourne.
- ↑ Ellingham, M. N.; Horton, J. D. (1983), "Non-Hamiltonian 3-connected cubic bipartite graphs", Journal of Combinatorial Theory, Series B 34 (3): 350–353, doi:10.1016/0095-8956(83)90046-1.
- ↑ Georges, J. P. (1989), "Non-hamiltonian bicubic graphs", Journal of Combinatorial Theory, Series B 46 (1): 121–124, doi:10.1016/0095-8956(89)90012-9.
 |