Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each internal vertex are equal to each other.[1] A regular graph with vertices of degree k is called a k‑regular graph or regular graph of degree k.
Special cases
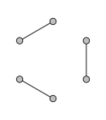
Regular graphs of degree at most 2 are easy to classify: a 0-regular graph consists of disconnected vertices, a 1-regular graph consists of disconnected edges, and a 2-regular graph consists of a disjoint union of cycles and infinite chains.
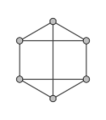
In analogy with the terminology for polynomials of low degrees, a 3-regular or 4-regular graph often is called a cubic graph or a quartic graph, respectively. Similarly, it is possible to denote k-regular graphs with as quintic, sextic, septic, octic, et cetera.
A strongly regular graph is a regular graph where every adjacent pair of vertices has the same number l of neighbors in common, and every non-adjacent pair of vertices has the same number n of neighbors in common. The smallest graphs that are regular but not strongly regular are the cycle graph and the circulant graph on 6 vertices.
The complete graph Km is strongly regular for any m.
-
0-regular graph
-
1-regular graph
-
2-regular graph
-
3-regular graph
Properties
By the degree sum formula, a k-regular graph with n vertices has edges. In particular, at least one of the order n and the degree k must be an even number.
A theorem by Nash-Williams says that every k‑regular graph on 2k + 1 vertices has a Hamiltonian cycle.
Let A be the adjacency matrix of a graph. Then the graph is regular if and only if is an eigenvector of A.[2] Its eigenvalue will be the constant degree of the graph. Eigenvectors corresponding to other eigenvalues are orthogonal to , so for such eigenvectors , we have .
A regular graph of degree k is connected if and only if the eigenvalue k has multiplicity one. The "only if" direction is a consequence of the Perron–Frobenius theorem.[2]
There is also a criterion for regular and connected graphs : a graph is connected and regular if and only if the matrix of ones J, with , is in the adjacency algebra of the graph (meaning it is a linear combination of powers of A).[3]
Let G be a k-regular graph with diameter D and eigenvalues of adjacency matrix . If G is not bipartite, then
Existence
There exists a -regular graph of order if and only if the natural numbers n and k satisfy the inequality and that is even.
Proof: If a graph with n vertices is k-regular, then the degree k of any vertex v cannot exceed the number of vertices different from v, and indeed at least one of n and k must be even, whence so is their product.
Conversely, if n and k are two natural numbers satisfying both the inequality and the parity condition, then indeed there is a k-regular circulant graph of order n (where the denote the minimal `jumps' such that vertices with indices differing by an are adjacent). If in addition k is even, then , and a possible choice is . Else k is odd, whence n must be even, say with , and then and the `jumps' may be chosen as .
If , then this circulant graph is complete.
Generation
Fast algorithms exist to generate, up to isomorphism, all regular graphs with a given degree and number of vertices.[5]
See also
References
- ↑ Chen, Wai-Kai (1997). Graph Theory and its Engineering Applications. World Scientific. pp. 29. ISBN 978-981-02-1859-1. https://archive.org/details/graphtheoryitsen00chen/page/29.
- ↑ 2.0 2.1 Cvetković, D. M.; Doob, M.; and Sachs, H. Spectra of Graphs: Theory and Applications, 3rd rev. enl. ed. New York: Wiley, 1998.
- ↑ Curtin, Brian (2005), "Algebraic characterizations of graph regularity conditions", Designs, Codes and Cryptography 34 (2–3): 241–248, doi:10.1007/s10623-004-4857-4.
- ↑ Quenell, G. (1994-06-01). "Spectral Diameter Estimates for k-Regular Graphs". Advances in Mathematics 106 (1): 122–148. doi:10.1006/aima.1994.1052. ISSN 0001-8708. https://www.sciencedirect.com/science/article/pii/S0001870884710528. Retrieved 2025-04-10.[1]
- ↑ Meringer, Markus (1999). "Fast generation of regular graphs and construction of cages". Journal of Graph Theory 30 (2): 137–146. doi:10.1002/(SICI)1097-0118(199902)30:2<137::AID-JGT7>3.0.CO;2-G. http://www.mathe2.uni-bayreuth.de/markus/pdf/pub/FastGenRegGraphJGT.pdf.
External links
- Weisstein, Eric W.. "Regular Graph". http://mathworld.wolfram.com/RegularGraph.html.
- Weisstein, Eric W.. "Strongly Regular Graph". http://mathworld.wolfram.com/StronglyRegularGraph.html.
- GenReg software and data by Markus Meringer.
- Nash-Williams, Crispin (1969), Valency Sequences which force graphs to have Hamiltonian Circuits, University of Waterloo Research Report, Waterloo, Ontario: University of Waterloo
 |