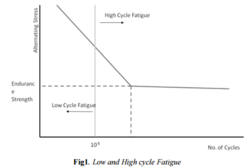
Engineering:Low-cycle fatigue
Low cycle fatigue (LCF) has two fundamental characteristics: plastic deformation in each cycle; and low cycle phenomenon, in which the materials have finite endurance for this type of load. The term cycle refers to repeated applications of stress that lead to eventual fatigue and failure; low-cycle pertains to a long period between applications. Study in fatigue has been focusing on mainly two fields: size design in aeronautics and energy production using advanced calculation methods. The LCF result allows us to study the behavior of the material in greater depth to better understand the complex mechanical and metallurgical phenomena (crack propagation, work softening, strain concentration, work hardening, etc.).[1]
History
Common factors that have been attributed to low-cycle fatigue (LCF) are high stress levels and a low number of cycles to failure. Many studies have been carried out, particularly in the last 50 years on metals and the relationship between temperature, stress, and number of cycles to failure. Tests are used to plot an S-N curve, and it has been shown that the number of cycles to failure decreased with increasing temperature. However, extensive testing would have been too costly so researchers mainly resorted to using finite element analysis using computer software.[2]
Through many experiments, it has been found that characteristics of a material can change as a result of LCF. Fracture ductility tends to decrease, with the magnitude depending on the presence of small cracks to begin with. To perform these tests, an electro-hydraulic servo-controlled testing machine was generally used, as it is capable of not changing the stress amplitude. It was also discovered that performing low-cycle fatigue tests on specimens with holes already drilled in them were more susceptible to crack propagation, and hence a greater decrease in fracture ductility. This was true despite the small hole sizes, ranging from 40 to 200 μm.[3]
Characteristics
When a component is subject to low cycle fatigue, it is repeatedly plastically deformed. For example, if a part were to be loaded in tension until it was permanently deformed (plastically deformed), that would be considered one quarter cycle of low cycle fatigue, or LCF. In order to complete a full cycle the part would need to be deformed back into its original shape. The number of LCF cycles that a part can withstand before failing is much lower than that of regular fatigue.[4]
This condition of high cyclic strain is often the result of extreme operating conditions, such as high changes in temperature. Thermal stresses originating from an expansion or contraction of materials can exacerbate the loading conditions on a part and LCF characteristics can come into play.
Mechanics
A commonly used equation that describes the behavior of low-cycle fatigue is the Coffin-Manson relation (published by L. F. Coffin in 1954 and S. S. Manson in 1953):
- [math]\displaystyle{ \frac {\Delta \varepsilon_p} {2} = \varepsilon_f '(2N)^c + \frac {\varsigma_f'(2N)^b}{E} }[/math]
where,
- Δεp /2 is the plastic strain amplitude;
- εf' is an empirical constant known as the fatigue ductility coefficient defined by the strain intercept at 2N =1;
- 2N is the number of reversals to failure (N cycles);
- c is an empirical constant known as the fatigue ductility exponent, commonly ranging from -0.5 to -0.7. Small c results in long fatigue life.
- b is an empirical constant known as the fatigue brittleness exponent.
The first half of the equation indicates the Plastic region and the second half of the equation indicates elastic region. [5]
Morrow Approximation
In the above given Coffin-Manson relation the constant values (b and c) is determined by the given equations:
[math]\displaystyle{ c= \frac{-1}{1+5\acute{n}} }[/math]
[math]\displaystyle{ b=\frac{-\acute{n}}{1+5\acute{n}} }[/math]
Notable failures
One noteworthy event in which the failure was a result of LCF was the 1994 Northridge earthquake. Many buildings and bridges collapsed, and as a result over 9,000 people were injured.[6] Researchers at the University of Southern California analyzed the main areas of a ten-story building that were subjected to low-cycle fatigue. Unfortunately, there was limited experimental data available to directly construct a S-N curve for low-cycle fatigue, so most of the analysis consisted of plotting the high-cycle fatigue behavior on a S-N curve and extending the line for that graph to create the portion of the low-cycle fatigue curve using the Palmgren-Miner method. Ultimately, this data was used to more accurately predict and analyze similar types of damage that the ten-story steel building in Northridge faced.[7]
Another more recent event was the 2010 Chile earthquake, in which several researchers from the University of Chile made reports of multiple reinforced concrete structures damaged throughout the country by the seismic event. Many structural elements such as beams, walls and columns failed due to fatigue, exposing the steel reinforcements used in the design with clear signs of longitudinal buckling.[9][10] This event caused Chilean seismic design standards to be updated based on observations on damaged structures caused by the earthquake.[11]
References
- ↑ Pineau, Andre (2013). "Low-Cycle Fatigue". Fatigue of Materials and Structures: Fundamentals: 113–177. doi:10.1002/9781118623435.ch4. ISBN 9781848210516.
- ↑ Agrawal, Richa (July 2014). "Low Cycle Fatigue Life Prediction". Richa Agrawal. http://www.ijeert.org/pdf/v2-i4/2.pdf.
- ↑ Murakami, Y.; Miller, K. J. (2005-08-01). "What is fatigue damage? A view point from the observation of low cycle fatigue process". International Journal of Fatigue. Cumulative Fatigue Damage Conference - University of Seville 2003 Cumulative Fatigue Damage Conference 27 (8): 991–1005. doi:10.1016/j.ijfatigue.2004.10.009.
- ↑ "Understanding Fatigue". D.P DeLuca. http://files.asme.org/IGTI/Knowledge/Articles/13048.pdf.
- ↑ O'Donnell, W.J. and B.F. Langer. Nuclear Science and Engineering, Vol 20, pp. 1-12, 1964.
- ↑ Taylor, Alan. "The Northridge Earthquake: 20 Years Ago Today" (in en-US). https://www.theatlantic.com/photo/2014/01/the-northridge-earthquake-20-years-ago-today/100664/.
- ↑ Nastar, Navid (2008). "Effects of Low-Cycle Fatigue on a Ten-Story Steel Building". http://bjsce.com/docs/LATBSDC_Paper.pdf.
- ↑ Rojas, F. (2011). "Performance of tall buildings in Concepción during the 27 February 2010 moment magnitude 8.8 offshore Maule, Chile earthquake". The Structural Design of Tall and Special Buildings 20 (37–64): 37–64. doi:10.1002/tal.674. https://onlinelibrary.wiley.com/doi/10.1002/tal.674.
- ↑ Egger, J. E.; Rojas, F. R.; Massone, L. M. (2021-09-24). "High-Strength Reinforcing Steel Bars: Low Cycle Fatigue Behavior Using RGB Methodology". International Journal of Concrete Structures and Materials 15 (38). doi:10.1186/s40069-021-00474-9.
- ↑ Massone, L. M.; Herrera, P.A. (2019-05-22). "Experimental study of the residual fatigue life of reinforcement bars damaged by an earthquake". Materials and Structures 52 (61). doi:10.1617/s11527-019-1361-x. https://link.springer.com/article/10.1617/s11527-019-1361-x.
- ↑ Wallace, John W.; Massone, Leonardo M.; Bonelli, Patricio; Dragovich, Jeff; Lagos, René; Lüders, Carl; Moehle, Jack (2012). "Damage and implications for seismic design of RC structural wall buildings". Earthquake Spectra (Wallace J, Massone L, Bonelli P, Dragovich J, Lagos R, Lüders C, Moehle J) 28: 281–299. doi:10.1193/1.4000047. https://doi.org/10.1193/1.4000047.
 |