Engineering:Phase-locked loop range

From HandWiki
Short description: Parameter of phase-locked loop engineering

The terms hold-in range, pull-in range (acquisition range), and lock-in range are widely used by engineers for the concepts of frequency deviation ranges within which phase-locked loop-based circuits can achieve lock under various additional conditions.

History

In the classic books on phase-locked loops,[1][2] published in 1966, such concepts as hold-in, pull-in, lock-in, and other frequency ranges for which PLL can achieve lock, were introduced. They are widely used nowadays (see, e.g. contemporary engineering literature[3][4] and other publications). Usually in engineering literature only non-strict definitions are given for these concepts. Many years of using definitions based on the above concepts has led to the advice given in a handbook on synchronization and communications, namely to check the definitions carefully before using them.[5] Later some rigorous mathematical definitions were given in.[6][7]

Gardner problem on the lock-in range definition

In the 1st edition of his well-known work, Phaselock Techniques, Floyd M. Gardner introduced a lock-in concept:[8] If, for some reason, the frequency difference between input and VCO is less than the loop bandwidth, the loop will lock up almost instantaneously without slipping cycles. The maximum frequency difference for which this fast acquisition is possible is called the lock-in frequency. His notion of the lock-in frequency and corresponding definition of the lock-in range have become popular and nowadays are given in various engineering publications. However, since even for zero frequency difference there may exist initial states of loop such that cycle slipping may take place during the acquisition process, the consideration of initial state of the loop is of utmost importance for the cycle slip analysis and, therefore, Gardner’s concept of lock-in frequency lacked rigor and required clarification.

In the 2nd edition of his book, Gardner stated: "there is no natural way to define exactly any unique lock-in frequency", and he wrote that "despite its vague reality, lock-in range is a useful concept".[9][10]

Definitions

  • [math]\displaystyle{ \theta_\Delta(t) = \theta_\text{ref}(t) - \theta_\text{VCO}(t) }[/math] phase difference between input (reference) signal and local oscillator (VCO, NCO) signal.
  • [math]\displaystyle{ \theta_\Delta(0) }[/math] initial phase difference between input signal and VCO signal.
  • [math]\displaystyle{ \omega_\Delta(t) = \dot\theta_\text{ref}(t) - \dot\theta_\text{VCO}(t) }[/math] frequency difference between input signal frequency and VCO signal.
  • [math]\displaystyle{ \omega_\Delta^\text{free} = \omega_\text{ref} - \omega_\text{VCO}^\text{free} }[/math] frequency difference between input signal frequency and VCO free running frequency.

Note that in general [math]\displaystyle{ \omega_\Delta^\text{free} \neq \omega_\Delta(0) }[/math], because [math]\displaystyle{ \omega_\Delta(0) }[/math] also depends on initial input of VCO.

Locked state

Definition of locked state

In a locked state: 1) the phase error fluctuations are small, the frequency error is small; 2) PLL approaches the same locked state after small perturbations of the phases and filter state.

Hold-in range

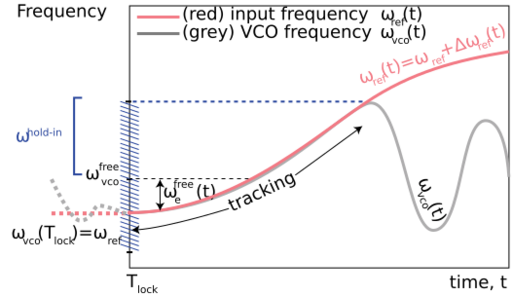
Hold-in range. Free-running frequency of VCO is fixed and input signal frequency is slowly-changing. While ω ref is inside hold-in range, VCO frequency is in tune with it, which is called tracking. Outside hold-in range VCO may unlock from input signal.

Definition of hold-in range.

A largest interval of frequency deviations [math]\displaystyle{ 0 \leq \left|\omega_\Delta^\text{free}\right| \leq \omega_h }[/math] for which a locked state exists is called a hold-in range, and [math]\displaystyle{ \omega_h }[/math] is called hold-in frequency.[6][7]

Value of frequency deviation belongs to the hold-in range if the loop re-achieves locked state after small perturbations of the filter's state, the phases and frequencies of VCO and the input signals. This effect is also called steady-state stability. In addition, for a frequency deviation within the hold-in range, after a small changes in input frequency loop re-achieves a new locked state (tracking process).

Pull-in range

Also called acquisition range, capture range.[11]

Assume that the loop power supply is initially switched off and then at [math]\displaystyle{ t = 0 }[/math] the power is switched on, and assume that the initial frequency difference is sufficiently large. The loop may not lock within one beat note, but the VCO frequency will be slowly tuned toward the reference frequency (acquisition process). This effect is also called a transient stability. The pull-in range is used to name such frequency deviations that make the acquisition process possible (see, for example, explanations in (Gardner 1966) and (Best 2007)).

Definition of pull-in range.

Pull-in range is a largest interval of frequency deviations [math]\displaystyle{ 0 \leq \left|\omega_\Delta^\text{free}\right| \leq \omega_p }[/math] such that PLL acquires lock for arbitrary initial phase, initial frequency, and filter state. Here [math]\displaystyle{ \omega_p }[/math] is called pull-in frequency.[6][7][12]

The difficulties of reliable numerical analysis of the pull-in range may be caused by the presence of hidden attractors in dynamical model of the circuit.[13][14][15]

Lock-in range

Assume that PLL is initially locked. Then the reference frequency [math]\displaystyle{ \omega_1 }[/math] is suddenly changed in an abrupt manner(step change). Pull-in range guarantees that PLL will eventually synchronize, however this process may take a long time. Such long acquisition process is called cycle slipping.

If difference between initial and final phase deviation is larger than [math]\displaystyle{ 2\pi }[/math], we say that cycle slipping takes place.

[math]\displaystyle{ \exist t \gt T_\text{lock}: \left|\theta_\Delta(0) - \theta_\Delta(t)\right| \geq 2\pi. }[/math]

Here, sometimes, the limit of the difference or the maximum of the difference is considered[16]

Definition of lock-in range.

If the loop is in a locked state, then after an abrupt change of [math]\displaystyle{ \omega_\Delta^\text{free} }[/math] free within a lock-in range [math]\displaystyle{ \left|\omega_\Delta^\text{free}\right| \leq \omega_\ell }[/math], the PLL acquires lock without cycle slipping. Here [math]\displaystyle{ \omega_\ell }[/math] is called lock-in frequency.[6][7][17]

References

  1. ↑ Phase-lock techniques.. New York: John Wiley & Sons. 1966. 
  2. ↑ Viterbi, A. (1966). Principles of coherent communications.. New York: McGraw-Hill. 
  3. ↑ Phase-lock techniques (3rd ed.). Wiley. 2005. 
  4. ↑ Best, Roland (2007). Phase-Lock Loops: Design, Simulation and Application (6th ed.). McGraw-Hill. 
  5. ↑ Kihara, M.; Ono, S.; Eskelinen, P. (2002). Digital Clocks for Synchronization and Communications.. Artech House. p. 49. 
  6. ↑ 6.0 6.1 6.2 6.3 Leonov, G. A.; Kuznetsov, N. V.; Yuldashev, M. V.; Yuldashev, R. V. (2015). "Hold-in, pull-in, and lock-in ranges of PLL circuits: rigorous mathematical definitions and limitations of classical theory.". IEEE Transactions on Circuits and Systems I: Regular Papers (IEEE) 62 (10): 2454–2464. doi:10.1109/TCSI.2015.2476295. 
  7. ↑ 7.0 7.1 7.2 7.3 Kuznetsov, N. V.; Leonov, G. A.; Yuldashev, M. V.; Yuldashev, R. V. (2015). "Rigorous mathematical definitions of the hold-in and pull-in ranges for phase-locked loops". IFAC-PapersOnLine 48 (11): 710–713. doi:10.1016/j.ifacol.2015.09.272. 
  8. ↑ Gardner 1966, p. 40
  9. ↑ Gardner, Floyd (1979). Phase-lock techniques (2nd ed.). New York: John Wiley & Sons. p. 70. 
  10. ↑ see also Gardner 2005, pp. 187–188
  11. ↑ Razavi, B. (1996). Design of Monolithic Phase-Locked Loops and Clock Recovery Circuits-A Tutorial.. IEEE Press. 
  12. ↑ Kuznetsov, N.V.; Lobachev, M.Y.; Yuldashev, M.V.; Yuldashev, R.V. (2021). "The Egan problem on the pull-in range of type 2 PLLs". IEEE Transactions on Circuits and Systems II: Express Briefs 68 (4): 1467–1471. doi:10.1109/TCSII.2020.3038075. 
  13. ↑ Kuznetsov, N.V.; Leonov, G.A.; Yuldashev, M.V.; Yuldashev, R.V. (2017). "Hidden attractors in dynamical models of phase-locked loop circuits: limitations of simulation in MATLAB and SPICE". Communications in Nonlinear Science and Numerical Simulation 51: 39–49. doi:10.1016/j.cnsns.2017.03.010. Bibcode: 2017CNSNS..51...39K. http://urn.fi/URN:NBN:fi:jyu-201704031870. 
  14. ↑ Best, R.; Kuznetsov, N.V.; Leonov, G.A.; Yuldashev, M.V.; Yuldashev, R.V. (2016). "Tutorial on dynamic analysis of the Costas loop". IFAC Annual Reviews in Control 42: 27–49. doi:10.1016/j.arcontrol.2016.08.003. https://zenodo.org/record/896255. 
  15. ↑ Kuznetsov, N.V.; Lobachev, M.V.; Yuldashev, M.V.; Yuldashev, R.V. (2019). "On the Gardner problem for phase-locked loops". Doklady Mathematics 100 (3): 568–570. doi:10.1134/S1064562419060218. 
  16. ↑ Stensby, J. (1997). Phase-Locked Loops: Theory and Applications.. Taylor & Francis. 
  17. ↑ Kuznetsov, N.V.; Lobachev, M.Y.; Yuldashev, M.V.; Yuldashev, R.V.; Tavazoei, M.S. (2023). "The Gardner problem on the lock-in range of second-order type 2 phase-locked loops". IEEE Transactions on Automatic Control: 1–15. doi:10.1109/TAC.2023.3277896. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Engineering:Phase-locked_loop_range&oldid=3232383"