Engineering:Photoconductance decay

Photoconductance decay or Photoconductivity decay (PCD or PC), is a non-destructive analytical technique used to measure the lifetime of minority charge carriers in a semiconductor, especially in silicon wafers. The technique studies the transient photoconductivity of a semiconductor sample during or after it is illuminated by a light pulse. Electron–hole pairs are first generated by the light pulse, and the photoconductivity of the sample declines as the carriers recombine.

PCD is an important characterisation step in determining the quality and expected performance of wafers before they are used to fabricate devices such as integrated circuits or solar cells. It is one of the most common methods of determining carrier lifetimes.

PCD uses a fast light source (e.g. a xenon flash lamp) to excite the test sample, causing free carriers to be generated. Excess carriers in the material cause it to become more conductive, and thus the number of excess carriers ([math]\displaystyle{ \Delta n }[/math]) can be measured over time by measuring the material conductivity. Conductivity can be measured through non-contact methods, such as through microwave reflectance, or inductive or capacitive coupling. A higher effective lifetime of minority charge carriers indicate that they can remain mobile in the wafer for a long time period before undergoing recombination.

History

Characterisation of minority carrier lifetimes through measurement of photoconductance decay was a technique used by Bell Laboratories as early as 1954 on silicon and germanium wafers during investigation of carrier trapping. A detailed method for measuring PCD was published soon after by MIT Lincoln Laboratory in 1955. A standard method for PCD was described in ATSM standards in 1971 for measurement of minority carrier lifetimes. A new method for Quasi-steady-state photoconductance measurements was described in 1996 by Ronald Sinton.

Theory

A chart of Minority Carrier Lifetime vs. Minority Carrier Density used in Photoconductance decay measurement of a monocrystalline silicon wafer passivated with an amorphous silicon thin layer.

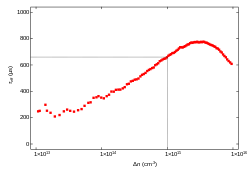
The difference in dark and excited photoconductivity [math]\displaystyle{ \Delta \sigma }[/math] of the wafer is typically measured through monitoring of the voltage across the induction coil beneath the wafer. This yields a conductance that is spatially averaged over the coil area. Conductance can be related to the excess carrier generation by;

[math]\displaystyle{ \Delta\sigma = q(\mu_n \Delta n + \mu_p \Delta p)W }[/math]

where [math]\displaystyle{ \Delta n }[/math] and [math]\displaystyle{ \Delta p }[/math] are excess electrons and holes, [math]\displaystyle{ \mu_n }[/math] and [math]\displaystyle{ \mu_p }[/math] are the electron and hole mobilities respectively, [math]\displaystyle{ W }[/math] is the wafer thickness and [math]\displaystyle{ q }[/math] is the elementary charge. It can be assumed that [math]\displaystyle{ \Delta n = \Delta p }[/math] as electrons and holes are always generated in pairs.

When the conductance is obtained, the average [math]\displaystyle{ \Delta n }[/math] can be calculated from the semiconductor parameters;

[math]\displaystyle{ \overline{\Delta n } = \frac{\Delta \sigma}{q(\mu_n + \mu_p)W} }[/math]

Depending on the expected lifetime of the material relative to the illumination decay characteristics of the flash lamp, there are several modes that can be used for PCD measurements.

The generalised equation for effective lifetimes [math]\displaystyle{ \tau_{eff} }[/math] as a function of the excess carrier density is given by;

[math]\displaystyle{ \tau_{eff}(\Delta n)=\frac{\Delta n(t)}{G(t) - \frac{\mathrm{d} \Delta n(t)}{\mathrm{d} t}} }[/math]

(1)

where [math]\displaystyle{ G(t) }[/math] is the generation rate as measured by a photodetector. The generalised case can be used regardless of the wafer lifetime or flash lamp.

Alternatively, the limiting cases of this function can be exploited in either quasi-transient or quasi-steady-state photoconductance (QSS-PC) measurements.

Transient PCD is used when the [math]\displaystyle{ \tau_{eff} }[/math] of the material is expected to exceed the flash duration, and the PCD measurement is taken after the light source has completely decayed. In this case, [math]\displaystyle{ G(t) }[/math] is assumed to be 0, and Equation (1) can be reduced to;

[math]\displaystyle{ \tau_{eff}(\Delta n)=-\frac{\Delta n(t)}{\frac{\mathrm{d} \Delta n(t)}{\mathrm{d} t}} }[/math]

For materials in which the effective lifetime is expected to be shorter than the flash lamp decay time, carriers are assumed to be continuously generated (i.e. at steady state), and therefore [math]\displaystyle{ \frac{\mathrm{d} \Delta n(t)}{\mathrm{d} t}=0 }[/math]. Therefore, Equation (1) can be reduced to;

[math]\displaystyle{ \tau_{eff}(\Delta n)=\frac{\Delta n(t)}{G(t)} }[/math]

The case to be used is determined experimentally. The effective lifetimes is then calculated through curve fitting of the function and evaluated at a specified minority carrier density set-point, typically [math]\displaystyle{ \Delta n = 1\times10^{15}\ {\rm cm^{-3}} }[/math] (see figure).

Applications

A PCD-calibrated photoluminescence image showing the change in passivation quality (lifetimes) after annealing a crystalline silicon wafer passivated with amorphous silicon, at varying temperatures

Recombination through the Shockley–Read–Hall (SRH) method is associated with the density of defects (such as contaminant atoms, dangling bonds, crystal grain boundaries, mechanical damage, etc.) in the semiconductor which "trap" charge carriers, leading to reduced lifetimes. Thus PCD can be used to infer the purity or passivation quality of the wafer. In solar cell production, this is particularly useful when estimating the performance of a precursor early in its manufacturing stage. Charge carriers that recombine cannot be used for photocurrent extraction, therefore for higher solar cell efficiency it is desirable to have a higher effective lifetime.

The minority carrier lifetime is also related to the open-circuit voltage of a solar cell, and therefore can be used to infer an implicit current–voltage characteristic of the finished solar cell.

Lifetimes measurements from PCD can be used to quantitatively calibrate spatially-resolved lifetimes measurements from Photoluminescence (PL) imaging. Minority carrier lifetimes are higher when there are fewer trap defects, and in the absence of SRH recombination, radiative recombination becomes more dominant. After excitation, radiatively recombining carriers emit nearly monochromatic light at the band gap energy of the semiconductor sample. For silicon, the energy is 1.12eV (in infrared) which can be captured by a CCD camera. Areas of the image with higher PL counts are inferred to have proportionately higher lifetimes.

See also

• Transient photocurrent