Engineering:Slip factor

Short description: Measure of the fluid slip in the impeller of a compressor or a turbine

In turbomachinery, the slip factor is a measure of the fluid slip in the impeller of a compressor or a turbine, mostly a centrifugal machine. Fluid slip is the deviation in the angle at which the fluid leaves the impeller from the impeller's blade/vane angle. Being quite small in axial impellers (inlet and outlet flow in the same direction), slip is a very important phenomenon in radial impellers and is useful in determining the accurate estimation of work input or the energy transfer between the impeller and the fluid, rise in pressure and the velocity triangles at the impeller exit.

A simple explanation for the fluid slip can be given as: Consider an impeller with z number of blades rotating at angular velocity ω. A difference in pressure and velocity during the course of clockwise flow through the impeller passage can be observed between the trailing and leading faces of the impeller blades. High pressure and low velocity are observed at the leading face of the impeller's blade as compared to lower pressure with high velocity at the trailing face of the blade. This results in circulation in the direction of ω around the impeller blade which prevents the air from acquiring the whirl velocity equivalent to impeller speed with non-uniform velocity distribution at any radius.

This phenomenon reduces the output whirl velocity, which is a measure of the net power output from a turbine or a compressor. Hence, the slip factor accommodates for a slip loss which affects the net power developed which increases with increasing flow-rate.

Factors accounting for slip factor

• Relative eddy.
• Back eddy.
• Impeller design or geometry

1. Mean blade loading.
2. Thickness of blade.
3. Finite number of blades.

• Fluid entry conditions.
• Working fluid's viscosity.
• Effect of boundary layer growth.
• Flow separation.
• Friction forces on the walls of flow packages.
• Boundary layer blockage.

Mathematical Formulae for Slip factor

Fig 1. Ideal and Actual velocity triangles at impeller exit

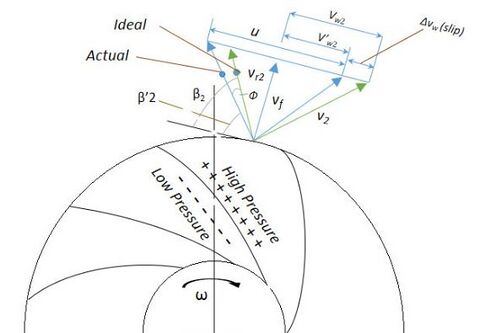
Mathematically, the Slip factor denoted by 'σ' is defined as the ratio of the actual & ideal values of the whirl velocity components at the exit of the impeller. The ideal values can be calculated using an analytical approach while the actual values should be observed experimentally.

[math]\displaystyle{ \sigma = \frac{V'_{w2}}{V_{w2}} }[/math]

where,

V'_w2 : Actual Whirl Velocity Component ,

V_w2  : Ideal Whirl Velocity Component

Usually,σ varies from 0-1 with an average ranging from 0.8-0.9.

The Slip Velocity is given as:

V_S = V_w2 - V'_w2 = V_w2(1-σ)

The Whirl Velocity is given as:

V'_w2 = σ V_w2

Slip Factor correlations

• Stodola's Equation: According to Stodola, it is the relative eddy that fills the entire exit session of the impeller passage. For a given flow geometry, the slip factor increases with the increase in the number of impeller blades, thus, accounts for one of the important parameter for losses.

[math]\displaystyle{ \sigma = 1-\frac\pi{z}\frac{\sin\beta_2}{(1-\phi_2\cot\beta_2)} }[/math]

where, z = number of blades and [math]\displaystyle{ \phi_2 = \frac{V_{r2}}{U_{2}} }[/math]

For Radial tip, β₂ = 90⁰ ∴ [math]\displaystyle{ \sigma = 1-\frac\pi{z} }[/math]

Theoretically, In order to get the perfect ideal flow guidance, one can infinitesimally increase the number of thin vanes so that the flow should leave the impeller at an exact vane angle.

However, later experiments proved that beyond a particular value, a further increase in number of blades results in reduction of slip factor due to increase in blockage area.

• Stanitz's Equation: Stanitz found the slip velocity does not depend upon the blade exit angle and hence, gave the following equation.

[math]\displaystyle{ \sigma = 1-\frac{1.98}{z(1-\phi_2\cot\beta_2)} }[/math]

where, z = number of blades,

β₂ varies from 45⁰ to 90⁰.

For radial tip: β₂ = 90⁰ ∴ [math]\displaystyle{ \sigma = 1-\frac{1.98}{z} = 1- \frac{0.63*pi}{z} }[/math]

• Balje's formula: An approximate formula given by Balje for radial-tipped (β₂=90⁰) blade impellers:

[math]\displaystyle{ \sigma = [1+\frac{6.2}{z.n^{2/3}}]^{-1} }[/math]

where, z = number of blades , n = [math]\displaystyle{ \frac{Impeller\ Tip\ Diameter}{Eye\ Tip\ Diameter} }[/math]

The above explained models clearly states that the Slip factor is solely a function of geometry of Impeller. However, later studies proved that Slip factor depends on other factors as well namely 'mass flow rate',viscosity etc..

See also

• Physics:Boundary layer – Layer of fluid in the immediate vicinity of a bounding surface
• Physics:Fluid mechanics – Branch of physics concerned with the mechanics of fluids (liquids, gases, and plasmas)
• Physics:Flow separation – Detachment of a boundary layer from a surface into a wake

Notes

• It is found that the downfall in blade angle towards the impeller exit results in increment of slip factor with increasing flow rate and vice versa.
• Slip Factor being a function of mass flow rate because of back eddy.

References

1. Flow simulation in radial pump impellers and evaluation of slip factor (July, 2015), http://pia.sagepub.com/content/early/2015/07/08/0957650915594953.full.pdf?ijkey=pW8QmRIKoDzyXzO&keytype=finite.
2. Seppo A. Korpela (2011), Principles of Turbomachinery. John Wiley & Sons, Inc. ISBN:978-0-470-53672-8.
3. S.L. Dixon (1998), Fluid Mechanics And Thermodynamics of Turbomachinery. Elsevier Butterworth-Heinemann, Inc. ISBN:0-7506-7870-4.
4. Rama Gorla, Aijaz Khan, Turbomachinery:Design and Theory. Marcel Dekker, Inc. ISBN:0-8247-0980-2.
5. Fluid Machine - FKM
6. Analysis and Validation of a Unified Slip Factor Model for Impellers at Design and off-Design Conditions
7. Numerical Study of Slip Factor in Centrifugal Pumps and Study Factors Affecting its Performance
8. Fluid Machinery - NPTEL
9. Experimental and Analytical Investigations of Slip Factor In Radial Tipped Centrifugal Fan.