Engineering:Tesla valve

From HandWiki
Short description: Valve design
A line drawing of the valve
Cross-section of a Tesla valve, displaying its cavity design, from the original patent application.
Streakline flow visualization at Re=200 using dye injected upstream:

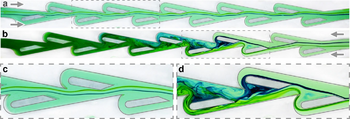
(a) Forward direction. Two adjacent filaments remain in the central corridor of the conduit with only small lateral deflections.

(b) Reverse direction. The filaments ricochet off the periodic structures, deflecting increasingly sharply before being rerouted around the 'islands' and mixing.
(c) and (d) are zoomed-in images

A Tesla valve, called a valvular conduit by its inventor, is a fixed-geometry passive check valve. It allows a fluid to flow preferentially in one direction, without moving parts. The device is named after Nikola Tesla, who was awarded U.S. Patent 1,329,559 in 1920 for its invention. The patent application describes the invention as follows:[1]

The interior of the conduit is provided with enlargements, recesses, projections, baffles, or buckets which, while offering virtually no resistance to the passage of the fluid in one direction, other than surface friction, constitute an almost impassable barrier to its flow in the opposite direction.

Tesla illustrated this with the drawing, showing one possible construction with a series of eleven flow-control segments, although any other number of such segments could be used as desired to increase or decrease the flow regulation effect.

With no moving parts, Tesla valves are much more resistant to wear and fatigue, especially in applications with frequent pressure reversal such as a pulsejet.[2]

A micrograph of a Tesla valve in a fixed-valve micro-pump, with flow from right to left restricted[3]

The Tesla valve is used in microfluidic applications[4] and offers advantages such as scalability, durability, and ease of fabrication in a variety of materials.[5] It is also used in macrofluidic applications and pulse jet engines.[6]

Principle of operation of a Tesla valve:
The upper figure shows flow in the blocking direction: at each segment, part of the fluid is turned around (red) and interferes with the forward flow (black).
The lower figure shows flow in the unimpeded direction (blue).

One computational fluid dynamics simulation of Tesla valves with two and four segments showed that the flow resistance in the blocking (or reverse) direction was about 15 and 40 times greater, respectively, than the unimpeded (or forward) direction.[7] This lends support to Tesla's patent assertion that in the valvular conduit in his diagram, a pressure ratio "approximating 200 can be obtained so that the device acts as a slightly leaking valve".[1]

Steady flow experiments, including with the original design, however, show smaller ratios of the two resistances in the range of 2 to 4.[6] It has also been shown that the device works better with pulsatile flows.[6]

Diodicity

The valves are structures that have a higher pressure drop for the flow in one direction (reverse) than the other (forward). This difference in flow resistance causes a net directional flow rate in the forward direction in oscillating flows. The efficiency is often expressed in diodicity [math]\displaystyle{ \mathrm{Di} }[/math], being the ratio of directional resistances.

The flow resistance is defined, analogously to Ohm's law for electrical resistance,[8] as the ratio of applied pressure drop and resulted flow rate:

[math]\displaystyle{ R = \frac{\Delta p}{Q} }[/math] where [math]\displaystyle{ \Delta p }[/math] is the applied pressure difference between two ends of the conduit, and [math]\displaystyle{ Q }[/math] the flow rate.

The diodicity is then the ratio of the reversed flow resistance to the forward flow resistance: [math]\displaystyle{ \mathrm {Di} = \frac{R_{\rm r}}{R_{\rm f}} }[/math]. If [math]\displaystyle{ \mathrm {Di} \gt 1 }[/math], the conduit in question has diodic behavior.

Thus diodicity is also the ratio of pressure drops for identical flow rates:[9]

[math]\displaystyle{ \mathrm {Di} = \left( \frac{\Delta p_{\rm r}}{\Delta p_{\rm f}} \right)_Q, }[/math]

where [math]\displaystyle{ \Delta p_{\rm r} }[/math] is the reverse flow pressure drop, and [math]\displaystyle{ \Delta p_{\rm f} }[/math] the forward flow pressure drop for flow rate [math]\displaystyle{ Q }[/math].

Equivalently, diodicity could also be defined as ratio of dimensionless Hagen number or Darcy friction factor at the same Reynolds number.[6]

See also

References

  1. ↑ 1.0 1.1 "Patent #: US001329559". Office of the Chief Communications Officer. http://pdfpiw.uspto.gov/.piw?PageNum=0&docid=01329559&IDKey=BD3AA70D843B%0D%0A&HomeUrl=http%3A%2F%2Fpatft.uspto.gov%2Fnetacgi%2Fnph-Parser%3FSect1%3DPTO1%2526Sect2%3DHITOFF%2526d%3DPALL%2526p%3D1%2526u%3D%25252Fnetahtml%25252FPTO%25252Fsrchnum.htm%2526r%3D1%2526f%3DG%2526l%3D50%2526s1%3D1329559.PN.%2526OS%3DPN%2F1329559%2526RS%3DPN%2F1329559. Retrieved 2 January 2017. 
  2. ↑ Mohammadzadeh, K.; Kolahdouz, Ebrahim M.; Shirani, E.; Shafii, M. B. (2013). "Numerical study on the performance of Tesla type microvalve in a valveless micropump in the range of low frequencies". Journal of Micro-Bio Robotics 8 (3–4): 145–159. doi:10.1007/s12213-013-0069-1. http://link.springer.com/article/10.1007/s12213-013-0069-1. Retrieved 2021-05-12. 
  3. ↑ Forster, Fred K.; Bardell, Ronald L.; Afromowitz, Martin A.; Sharma, Nigel R. (1995). "Design, fabrication and testing of fixed-valve micro-pumps". 234. pp. 39–44. https://www.researchgate.net/publication/245883107. 
  4. ↑ Deng, Yongbo; Liu, Zhenyu; Zhang, Ping (28 Jan 2010). "Optimization of no-moving part fluidic resistance microvalves with low reynolds number". 2010 IEEE 23rd International Conference on Micro Electro Mechanical Systems (MEMS). pp. 67–70. doi:10.1109/MEMSYS.2010.5442565. ISBN 978-1-4244-5761-8. https://www.researchgate.net/publication/224129251. Retrieved 12 May 2021. 
  5. ↑ Gamboa, Adrian R.; Morris, Christopher J.; Forster, Fred K. (2005). "Improvements in Fixed-Valve Micropump Performance Through Shape Optimization of Valves". Journal of Fluids Engineering 127 (2): 339. doi:10.1115/1.1891151. 
  6. ↑ 6.0 6.1 6.2 6.3 Nguyen, Quynh M.; Abouezzi, Joanna; Ristroph, Leif (17 May 2021). "Early turbulence and pulsatile flows enhance diodicity of Tesla's macrofluidic valve". Nature Communications 12 (12): 2884. doi:10.1038/s41467-021-23009-y. PMID 34001882. Bibcode: 2021NatCo..12.2884N. 
  7. ↑ "Tesla's Valvular Conduit - Fluid Power Journal" (in en-US). 2013-10-23. https://fluidpowerjournal.com/2013/10/teslas-conduit/. 
  8. ↑ Nguyen, Quynh M.; Huang, Dean; Dean, Evan; Romanelli, Genievieve; Meyer, Charlotte; Ristroph, Leif (Oct 2020). "Tesla's fluidic diode and the electronic-hydraulic analogy". American Journal of Physics 89 (4): 393–402. doi:10.1119/10.0003395. 
  9. ↑ de Vries; Florea; Homburg; Frijns (2017). "Design and operation of a tesla-type valve for pulsating heat pipes". International Journal of Heat and Mass Transfer 105: 1–11. doi:10.1016/j.ijheatmasstransfer.2016.09.062. 

External links

] on YouTube

] on YouTube



Retrieved from "https://handwiki.org/wiki/index.php?title=Engineering:Tesla_valve&oldid=3262686"