Engineering:Van der Meer formula
The Van der Meer formula is a formula for calculating the required stone weight for armourstone under the influence of (wind) waves. This is necessary for the design of breakwaters and shoreline protection. Around 1985 it was found that the Hudson formula in use at that time had considerable limitations (only valid for permeable breakwaters and steep (storm) waves). That is why the Dutch government agency Rijkswaterstaat commissioned Deltares to start research for a more complete formula. This research, conducted by Jentsje van der Meer, resulted in the Van der Meer formula in 1988, as described in his dissertation.[1] This formula reads [2] [3]
- [math]\displaystyle{ \frac{H_s}{\Delta \cdot d_{n50}}= \begin{cases} c_{p} P^{0.18} \left (\frac{S}{\sqrt{N}} \right)^{0.2} \xi_m^{-0.5} & \mbox{when } \xi_m \lt \xi{cr} \quad [plunging] \\ c_{s} P^{-0.13} \left (\frac{S}{\sqrt{N}} \right)^{0.2} \xi_m^{P} \sqrt{cot \alpha} & \mbox{when } \xi_m \ge \xi{cr} \quad [surging] \end{cases} }[/math]
and
- [math]\displaystyle{ \xi_{cr} = \left[ \frac{c_p}{c_s}P^{0.31} \sqrt{tan \alpha} \right]^{\frac{1}{P+0.5}} }[/math]
In this formula:
- Hs = Significant wave height at the toe of the construction
- Δ = relative density of the stone (= (ρs -ρw)/ρw) where ρs is the density of the stone and ρw is the density of the water
- dn50 = nominal stone diameter
- α = breakwater slope
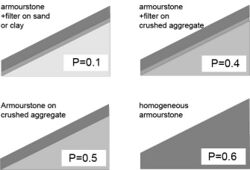
- P = notional permeability
- S = Damage number
- N = number of waves in the storm
- ξm = the Iribarren number calculated with the Tm
For design purposes, for the coefficient cp the value of 5,2 and for cs the value 0,87 is recommended.[2]
The value of P can be read from attached graph. Until now, there is no good method for determining P different than with accompanying pictures. Research is under way to try to determine the value of P using calculation models that can simulate the water movement in the breakwater (OpenFOAM models).
The value of the damage number S is defined as
- [math]\displaystyle{ S=\frac{A}{d_{n50}^2} }[/math][4]
where A is the area of the erosion area. Permissible values for S are:[2]
| slope | Start of damage | Average damage, repair needed | Failure (core is exposed)) |
|---|---|---|---|
| 1:1,5 | 2 | 3-5 | 8 |
| 1:2 | 2 | 4-6 | 8 |
| 1:3 | 2 | 6-9 | 12 |
| 1:4 | 3 | 8-12 | 17 |
| 1:6 | 3 | 8-12 | 17 |
References
- ↑ Van der Meer, J.W. (1988). Rock slopes and gravel beaches under wave attack. TU Delft and Deltares. pp. 214 p. http://resolver.tudelft.nl/uuid:67e5692c-0905-4ddd-8487-37fdda9af6b4.
- ↑ 2.0 2.1 2.2 CIRIA, CUR, CETMEF (2007). "5". The rock manual : the use of rock in hydraulic engineering. London: CIRIA C683. pp. 567–577. ISBN 9780860176831. http://kennisbank-waterbouw.tudelft.nl/DesignCodes/rockmanual/.
- ↑ Coastal Engineering Manual EM 1110-2-1100, part VI,chapter 5. US Army Corps of Engineers. 2011. p. 74. https://www.publications.usace.army.mil/USACE-Publications/Engineer-Manuals/u43544q/.
- ↑ Broderick, L.L. (1983). "Riprap stability, a progress report". American Society of Civil Engineering. pp. 320–330.
 |