Equal incircles theorem
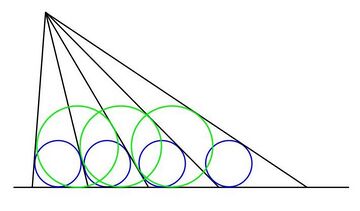
In geometry, the equal incircles theorem derives from a Japanese Sangaku, and pertains to the following construction: a series of rays are drawn from a given point to a given line such that the inscribed circles of the triangles formed by adjacent rays and the base line are equal. In the illustration the equal blue circles define the spacing between the rays, as described.
The theorem states that the incircles of the triangles formed (starting from any given ray) by every other ray, every third ray, etc. and the base line are also equal. The case of every other ray is illustrated above by the green circles, which are all equal.
From the fact that the theorem does not depend on the angle of the initial ray, it can be seen that the theorem properly belongs to analysis, rather than geometry, and must relate to a continuous scaling function which defines the spacing of the rays. In fact, this function is the hyperbolic sine.
The theorem is a direct corollary of the following lemma:
Suppose that the nth ray makes an angle [math]\displaystyle{ \gamma_n }[/math] with the normal to the baseline. If [math]\displaystyle{ \gamma_n }[/math] is parameterized according to the equation, [math]\displaystyle{ \tan \gamma_n = \sinh\theta_n }[/math], then values of [math]\displaystyle{ \theta_n = a + nb }[/math], where [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] are real constants, define a sequence of rays that satisfy the condition of equal incircles, and furthermore any sequence of rays satisfying the condition can be produced by suitable choice of the constants [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math].
Proof of the lemma
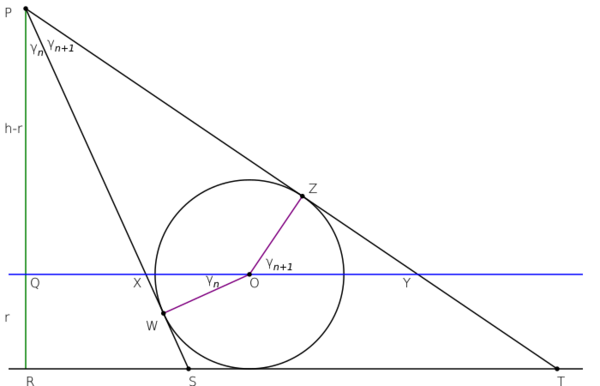
In the diagram, lines PS and PT are adjacent rays making angles [math]\displaystyle{ \gamma_n }[/math] and [math]\displaystyle{ \gamma_{n+1} }[/math] with line PR, which is perpendicular to the baseline, RST.
Line QXOY is parallel to the baseline and passes through O, the center of the incircle of [math]\displaystyle{ \triangle }[/math] PST, which is tangent to the rays at W and Z. Also, line PQ has length [math]\displaystyle{ h-r }[/math], and line QR has length [math]\displaystyle{ r }[/math], the radius of the incircle.
Then [math]\displaystyle{ \triangle }[/math] OWX is similar to [math]\displaystyle{ \triangle }[/math] PQX and [math]\displaystyle{ \triangle }[/math] OZY is similar to [math]\displaystyle{ \triangle }[/math] PQY, and from XY = XO + OY we get
- [math]\displaystyle{ (h-r) ( \tan \gamma_{n+1} - \tan \gamma_n ) = r ( \sec \gamma_n + \sec \gamma_{n+1} ). }[/math]
This relation on a set of angles, [math]\displaystyle{ \{ \gamma_m \} }[/math], expresses the condition of equal incircles.
To prove the lemma, we set [math]\displaystyle{ \tan \gamma_n = \sinh (a+nb) }[/math], which gives [math]\displaystyle{ \sec \gamma_n = \cosh(a+nb) }[/math].
Using [math]\displaystyle{ a+(n+1)b = (a+nb)+b }[/math], we apply the addition rules for [math]\displaystyle{ \sinh }[/math] and [math]\displaystyle{ \cosh }[/math], and verify that the equal incircles relation is satisfied by setting
- [math]\displaystyle{ \frac {r}{h-r} = \tanh\frac{b}{2}. }[/math]
This gives an expression for the parameter [math]\displaystyle{ b }[/math] in terms of the geometric measures, [math]\displaystyle{ h }[/math] and [math]\displaystyle{ r }[/math]. With this definition of [math]\displaystyle{ b }[/math] we then obtain an expression for the radii, [math]\displaystyle{ r_N }[/math], of the incircles formed by taking every Nth ray as the sides of the triangles
- [math]\displaystyle{ \frac {r_N}{h-r_N} = \tanh\frac{Nb}{2}. }[/math]
See also
- Hyperbolic function
- Japanese theorem for cyclic polygons
- Japanese theorem for cyclic quadrilaterals
- Tangent lines to circles
References
- Equal Incircles Theorem at cut-the-knot
- J. Tabov. A note on the five-circle theorem. Mathematics Magazine 63 (1989), 2, 92–94.
 |