Euclid's orchard

Short description: Array of line segments normal to points of a square lattice

Plan view of one corner of Euclid's orchard, in which trees are labelled with the x co-ordinate of their projection on the plane x + y = 1.

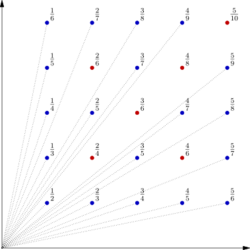
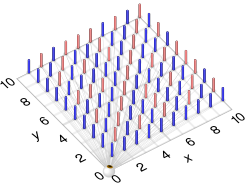
In mathematics, informally speaking, Euclid's orchard is an array of one-dimensional "trees" of unit height planted at the lattice points in one quadrant of a square lattice. More formally, Euclid's orchard is the set of line segments from (x, y, 0) to (x, y, 1), where x and y are positive integers.

One corner of Euclid's orchard, blue trees visible from the origin

Perspective view of Euclid's orchard from the origin. Red trees denote rows two off the main diagonal.

The trees visible from the origin are those at lattice points (x, y, 0), where x and y are coprime, i.e., where the fraction x/y is in reduced form. The name Euclid's orchard is derived from the Euclidean algorithm.

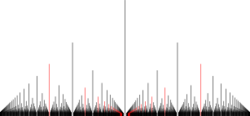
If the orchard is projected relative to the origin onto the plane x + y = 1 (or, equivalently, drawn in perspective from a viewpoint at the origin) the tops of the trees form a graph of Thomae's function. The point (x, y, 1) projects to

[math]\displaystyle{ \left ( \frac {x}{x+y}, \frac {y}{x+y}, \frac {1}{x+y} \right ). }[/math]

The solution to the Basel problem can be used to show that the proportion of points in the [math]\displaystyle{ n\times n }[/math] grid that have trees on them is approximately [math]\displaystyle{ \tfrac{6}{\pi^2} }[/math] and that the error of this approximation goes to zero in the limit as n goes to infinity.

See also

• Opaque forest problem

External links

• Euclid's Orchard, Grade 9-11 activities and problem sheet, Texas Instruments Inc.
• Project Euler related problem