Expander code

Expander codes
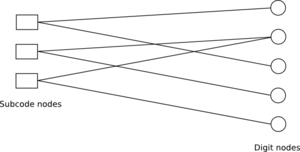bipartite expander graph
Classification
Type	Linear block code
Block length	[math]\displaystyle{ n }[/math]
Message length	[math]\displaystyle{ n-m }[/math]
Rate	[math]\displaystyle{ 1-m/n }[/math]
Distance	[math]\displaystyle{ 2(1-\epsilon)\gamma\cdot n }[/math]
Alphabet size	[math]\displaystyle{ 2 }[/math]
Notation	[math]\displaystyle{ [n,n-m,2(1-\epsilon)\gamma\cdot n]_2 }[/math]-code

In coding theory, expander codes form a class of error-correcting codes that are constructed from bipartite expander graphs. Along with Justesen codes, expander codes are of particular interest since they have a constant positive rate, a constant positive relative distance, and a constant alphabet size. In fact, the alphabet contains only two elements, so expander codes belong to the class of binary codes. Furthermore, expander codes can be both encoded and decoded in time proportional to the block length of the code.

Expander codes

In coding theory, an expander code is a [math]\displaystyle{ [n,n-m]_2\, }[/math] linear block code whose parity check matrix is the adjacency matrix of a bipartite expander graph. These codes have good relative distance [math]\displaystyle{ 2(1-\varepsilon)\gamma\, }[/math], where [math]\displaystyle{ \varepsilon\, }[/math] and [math]\displaystyle{ \gamma\, }[/math] are properties of the expander graph as defined later), rate [math]\displaystyle{ \left(1-\tfrac{m}{n}\right)\, }[/math], and decodability (algorithms of running time [math]\displaystyle{ O(n)\, }[/math] exist).

Definition

Let [math]\displaystyle{ B }[/math] be a [math]\displaystyle{ (c,d) }[/math]-biregular graph between a set of [math]\displaystyle{ n }[/math] nodes [math]\displaystyle{ \{v_1,\cdots,v_n\} }[/math], called variables, and a set of [math]\displaystyle{ cn/d }[/math] nodes [math]\displaystyle{ \{C_1,\cdots,C_{cn/d}\} }[/math], called constraints.

Let [math]\displaystyle{ b(i,j) }[/math] be a function designed so that, for each constraint [math]\displaystyle{ C_i }[/math], the variables neighboring [math]\displaystyle{ C_i }[/math] are [math]\displaystyle{ v_{b(i,1)},\cdots,v_{b(i,d)} }[/math].

Let [math]\displaystyle{ \mathcal{S} }[/math] be an error-correcting code of block length [math]\displaystyle{ d }[/math]. The expander code [math]\displaystyle{ \mathcal{C}(B,\mathcal{S}) }[/math] is the code of block length [math]\displaystyle{ n }[/math] whose codewords are the words [math]\displaystyle{ (x_1,\cdots,x_n) }[/math] such that, for [math]\displaystyle{ 1\leq i\leq cn/d }[/math], [math]\displaystyle{ (x_{b(i,1)},\cdots,x_{b(i,d)}) }[/math] is a codeword of [math]\displaystyle{ \mathcal{S} }[/math].

It has been shown that nontrivial lossless expander graphs exist. Moreover, we can explicitly construct them.

Rate

The rate of [math]\displaystyle{ C\, }[/math] is its dimension divided by its block length. In this case, the parity check matrix has size [math]\displaystyle{ m \times n\, }[/math], and hence [math]\displaystyle{ C\, }[/math] has rate at least [math]\displaystyle{ (n-m)/n = 1 - m/n\, }[/math].

Distance

Suppose [math]\displaystyle{ \varepsilon \lt \tfrac{1}{2}\, }[/math]. Then the distance of a [math]\displaystyle{ (n, m, d, \gamma, 1-\varepsilon)\, }[/math] expander code [math]\displaystyle{ C\, }[/math] is at least [math]\displaystyle{ 2(1-\varepsilon)\gamma n\, }[/math].

Proof

Note that we can consider every codeword [math]\displaystyle{ c\, }[/math] in [math]\displaystyle{ C\, }[/math] as a subset of vertices [math]\displaystyle{ S \subset L\, }[/math], by saying that vertex [math]\displaystyle{ v_i \in S\, }[/math] if and only if the [math]\displaystyle{ i\, }[/math]th index of the codeword is a 1. Then [math]\displaystyle{ c\, }[/math] is a codeword iff every vertex [math]\displaystyle{ v \in R\, }[/math] is adjacent to an even number of vertices in [math]\displaystyle{ S\, }[/math]. (In order to be a codeword, [math]\displaystyle{ cP = 0\, }[/math], where [math]\displaystyle{ P\, }[/math] is the parity check matrix. Then, each vertex in [math]\displaystyle{ R\, }[/math] corresponds to each column of [math]\displaystyle{ P\, }[/math]. Matrix multiplication over [math]\displaystyle{ \text{GF}(2) = \{0,1\}\, }[/math] then gives the desired result.) So, if a vertex [math]\displaystyle{ v \in R\, }[/math] is adjacent to a single vertex in [math]\displaystyle{ S\, }[/math], we know immediately that [math]\displaystyle{ c\, }[/math] is not a codeword. Let [math]\displaystyle{ N(S)\, }[/math] denote the neighbors in [math]\displaystyle{ R\, }[/math] of [math]\displaystyle{ S\, }[/math], and [math]\displaystyle{ U(S)\, }[/math] denote those neighbors of [math]\displaystyle{ S\, }[/math] which are unique, i.e., adjacent to a single vertex of [math]\displaystyle{ S\, }[/math].

Lemma 1

For every [math]\displaystyle{ S \subset L\, }[/math] of size [math]\displaystyle{ |S| \leq \gamma n\, }[/math], [math]\displaystyle{ d|S| \geq |N(S)| \geq |U(S)| \geq d(1-2\varepsilon)|S|\, }[/math].

Proof

Trivially, [math]\displaystyle{ |N(S)| \geq |U(S)|\, }[/math], since [math]\displaystyle{ v \in U(S)\, }[/math] implies [math]\displaystyle{ v \in N(S)\, }[/math]. [math]\displaystyle{ |N(S)| \leq d|S|\, }[/math] follows since the degree of every vertex in [math]\displaystyle{ S\, }[/math] is [math]\displaystyle{ d\, }[/math]. By the expansion property of the graph, there must be a set of [math]\displaystyle{ d(1-\varepsilon)|S|\, }[/math] edges which go to distinct vertices. The remaining [math]\displaystyle{ d\varepsilon|S|\, }[/math] edges make at most [math]\displaystyle{ d\varepsilon|S|\, }[/math] neighbors not unique, so [math]\displaystyle{ U(S) \geq d(1-\varepsilon)|S| - d\varepsilon|S| = d(1-2\varepsilon)|S|\, }[/math].

Corollary

Every sufficiently small [math]\displaystyle{ S\, }[/math] has a unique neighbor. This follows since [math]\displaystyle{ \varepsilon \lt \tfrac{1}{2}\, }[/math].

Lemma 2

Every subset [math]\displaystyle{ T \subset L\, }[/math] with [math]\displaystyle{ |T| \lt 2(1-\varepsilon)\gamma n\, }[/math] has a unique neighbor.

Proof

Lemma 1 proves the case [math]\displaystyle{ |T| \leq \gamma n\, }[/math], so suppose [math]\displaystyle{ 2(1-\varepsilon)\gamma n \gt |T| \gt \gamma n\, }[/math]. Let [math]\displaystyle{ S \subset T\, }[/math] such that [math]\displaystyle{ |S| = \gamma n\, }[/math]. By Lemma 1, we know that [math]\displaystyle{ |U(S)| \geq d(1-2\varepsilon)|S|\, }[/math]. Then a vertex [math]\displaystyle{ v \in U(S)\, }[/math] is in [math]\displaystyle{ U(T)\, }[/math] iff [math]\displaystyle{ v \notin N(T \setminus S)\, }[/math], and we know that [math]\displaystyle{ |T \setminus S| \leq 2(1-\varepsilon)\gamma n - \gamma n = (1-2\varepsilon)\gamma n\, }[/math], so by the first part of Lemma 1, we know [math]\displaystyle{ |N(T \setminus S)| \leq d(1-2\varepsilon)\gamma n\, }[/math]. Since [math]\displaystyle{ \varepsilon \lt \tfrac{1}{2}\, }[/math], [math]\displaystyle{ |U(T)| \geq |U(S) \setminus N(T \setminus S)| \geq |U(S)| - |N(T \setminus S)| \gt 0\, }[/math], and hence [math]\displaystyle{ U(T)\, }[/math] is not empty.

Corollary

Note that if a [math]\displaystyle{ T \subset L\, }[/math] has at least 1 unique neighbor, i.e. [math]\displaystyle{ |U(T)| \gt 0\, }[/math], then the corresponding word [math]\displaystyle{ c\, }[/math] corresponding to [math]\displaystyle{ T\, }[/math] cannot be a codeword, as it will not multiply to the all zeros vector by the parity check matrix. By the previous argument, [math]\displaystyle{ c \in C \implies wt(c) \geq 2(1-\varepsilon)\gamma n\, }[/math]. Since [math]\displaystyle{ C\, }[/math] is linear, we conclude that [math]\displaystyle{ C\, }[/math] has distance at least [math]\displaystyle{ 2(1-\varepsilon)\gamma n\, }[/math].

Encoding

The encoding time for an expander code is upper bounded by that of a general linear code - [math]\displaystyle{ O(n^2)\, }[/math] by matrix multiplication. A result due to Spielman shows that encoding is possible in [math]\displaystyle{ O(n)\, }[/math] time.

Decoding

Decoding of expander codes is possible in [math]\displaystyle{ O(n)\, }[/math] time when [math]\displaystyle{ \varepsilon \lt \tfrac{1}{4}\, }[/math] using the following algorithm.

Let [math]\displaystyle{ v_i\, }[/math] be the vertex of [math]\displaystyle{ L\, }[/math] that corresponds to the [math]\displaystyle{ i\, }[/math]th index in the codewords of [math]\displaystyle{ C\, }[/math]. Let [math]\displaystyle{ y \in \{0,1\}^n\, }[/math] be a received word, and [math]\displaystyle{ V(y) = \{v_i \mid \text{the } i^{\text{th}} \text{ position of } y \text{ is a } 1\}\, }[/math]. Let [math]\displaystyle{ e(i)\, }[/math] be [math]\displaystyle{ |\{v \in R \mid v_i \in N(v) \text{ and } N(v) \cap V(y) \text{ is even}\}|\, }[/math], and [math]\displaystyle{ o(i)\, }[/math] be [math]\displaystyle{ |\{v \in R \mid v_i \in N(v) \text{ and } N(v) \cap V(y) \text{ is odd}\}|\, }[/math]. Then consider the greedy algorithm:

---

Input: received word [math]\displaystyle{ y\, }[/math].

initialize y' to y
while there is a v in R adjacent to an odd number of vertices in V(y')
    if there is an i such that o(i) > e(i)
        flip entry i in y'
    else
        fail

Output: fail, or modified codeword [math]\displaystyle{ y'\, }[/math].

---

Proof

We show first the correctness of the algorithm, and then examine its running time.

Correctness

We must show that the algorithm terminates with the correct codeword when the received codeword is within half the code's distance of the original codeword. Let the set of corrupt variables be [math]\displaystyle{ S\, }[/math], [math]\displaystyle{ s = |S|\, }[/math], and the set of unsatisfied (adjacent to an odd number of vertices) vertices in [math]\displaystyle{ R\, }[/math] be [math]\displaystyle{ c\, }[/math]. The following lemma will prove useful.

Lemma 3

If [math]\displaystyle{ 0 \lt s \lt \gamma n\, }[/math], then there is a [math]\displaystyle{ v_i\, }[/math] with [math]\displaystyle{ o(i) \gt e(i)\, }[/math].

Proof

By Lemma 1, we know that [math]\displaystyle{ U(S) \geq d(1-2\varepsilon)s\, }[/math]. So an average vertex has at least [math]\displaystyle{ d(1-2\varepsilon) \gt d/2\, }[/math] unique neighbors (recall unique neighbors are unsatisfied and hence contribute to [math]\displaystyle{ o(i)\, }[/math]), since [math]\displaystyle{ \varepsilon \lt \tfrac{1}{4}\, }[/math], and thus there is a vertex [math]\displaystyle{ v_i\, }[/math] with [math]\displaystyle{ o(i) \gt e(i)\, }[/math].

So, if we have not yet reached a codeword, then there will always be some vertex to flip. Next, we show that the number of errors can never increase beyond [math]\displaystyle{ \gamma n\, }[/math].

Lemma 4

If we start with [math]\displaystyle{ s \lt \gamma(1-2\varepsilon)n\, }[/math], then we never reach [math]\displaystyle{ s = \gamma n\, }[/math] at any point in the algorithm.

Proof

When we flip a vertex [math]\displaystyle{ v_i\, }[/math], [math]\displaystyle{ o(i)\, }[/math] and [math]\displaystyle{ e(i)\, }[/math] are interchanged, and since we had [math]\displaystyle{ o(i) \gt e(i)\, }[/math], this means the number of unsatisfied vertices on the right decreases by at least one after each flip. Since [math]\displaystyle{ s \lt \gamma(1-2\varepsilon)n\, }[/math], the initial number of unsatisfied vertices is at most [math]\displaystyle{ d\gamma(1-2\varepsilon)n\, }[/math], by the graph's [math]\displaystyle{ d\, }[/math]-regularity. If we reached a string with [math]\displaystyle{ \gamma n\, }[/math] errors, then by Lemma 1, there would be at least [math]\displaystyle{ d\gamma(1-2\varepsilon)n\, }[/math] unique neighbors, which means there would be at least [math]\displaystyle{ d\gamma(1-2\varepsilon)n\, }[/math] unsatisfied vertices, a contradiction.

Lemmas 3 and 4 show us that if we start with [math]\displaystyle{ s \lt \gamma(1-2\varepsilon)n\, }[/math] (half the distance of [math]\displaystyle{ C\, }[/math]), then we will always find a vertex [math]\displaystyle{ v_i\, }[/math] to flip. Each flip reduces the number of unsatisfied vertices in [math]\displaystyle{ R\, }[/math] by at least 1, and hence the algorithm terminates in at most [math]\displaystyle{ m\, }[/math] steps, and it terminates at some codeword, by Lemma 3. (Were it not at a codeword, there would be some vertex to flip). Lemma 4 shows us that we can never be farther than [math]\displaystyle{ \gamma n\, }[/math] away from the correct codeword. Since the code has distance [math]\displaystyle{ 2(1-\varepsilon)\gamma n \gt \gamma n\, }[/math] (since [math]\displaystyle{ \varepsilon \lt \tfrac{1}{2}\, }[/math]), the codeword it terminates on must be the correct codeword, since the number of bit flips is less than half the distance (so we couldn't have traveled far enough to reach any other codeword).

Complexity

We now show that the algorithm can achieve linear time decoding. Let [math]\displaystyle{ \tfrac{n}{m}\, }[/math] be constant, and [math]\displaystyle{ r\, }[/math] be the maximum degree of any vertex in [math]\displaystyle{ R\, }[/math]. Note that [math]\displaystyle{ r\, }[/math] is also constant for known constructions.

1. Pre-processing: It takes [math]\displaystyle{ O(mr)\, }[/math] time to compute whether each vertex in [math]\displaystyle{ R\, }[/math] has an odd or even number of neighbors.
2. Pre-processing 2: We take [math]\displaystyle{ O(dn) = O(dmr)\, }[/math] time to compute a list of vertices [math]\displaystyle{ v_i\, }[/math] in [math]\displaystyle{ L\, }[/math] which have [math]\displaystyle{ o(i) \gt e(i)\, }[/math].
3. Each Iteration: We simply remove the first list element. To update the list of odd / even vertices in [math]\displaystyle{ R\, }[/math], we need only update [math]\displaystyle{ O(d)\, }[/math] entries, inserting / removing as necessary. We then update [math]\displaystyle{ O(dr)\, }[/math] entries in the list of vertices in [math]\displaystyle{ L\, }[/math] with more odd than even neighbors, inserting / removing as necessary. Thus each iteration takes [math]\displaystyle{ O(dr)\, }[/math] time.
4. As argued above, the total number of iterations is at most [math]\displaystyle{ m\, }[/math].

This gives a total runtime of [math]\displaystyle{ O(mdr) = O(n)\, }[/math] time, where [math]\displaystyle{ d\, }[/math] and [math]\displaystyle{ r\, }[/math] are constants.

See also

• Expander graph
• Low-density parity-check code
• Linear time encoding and decoding of error-correcting codes
• ABNNR and AEL codes

Notes

This article is based on Dr. Venkatesan Guruswami's course notes.