Factorization system
In mathematics, it can be shown that every function can be written as the composite of a surjective function followed by an injective function. Factorization systems are a generalization of this situation in category theory.
Definition
A factorization system (E, M) for a category C consists of two classes of morphisms E and M of C such that:
- E and M both contain all isomorphisms of C and are closed under composition.
- Every morphism f of C can be factored as [math]\displaystyle{ f=m\circ e }[/math] for some morphisms [math]\displaystyle{ e\in E }[/math] and [math]\displaystyle{ m\in M }[/math].
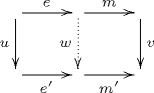
- The factorization is functorial: if [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] are two morphisms such that [math]\displaystyle{ vme=m'e'u }[/math] for some morphisms [math]\displaystyle{ e, e'\in E }[/math] and [math]\displaystyle{ m, m'\in M }[/math], then there exists a unique morphism [math]\displaystyle{ w }[/math] making the following diagram commute:
Remark: [math]\displaystyle{ (u,v) }[/math] is a morphism from [math]\displaystyle{ me }[/math] to [math]\displaystyle{ m'e' }[/math] in the arrow category.
Orthogonality
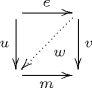
Two morphisms [math]\displaystyle{ e }[/math] and [math]\displaystyle{ m }[/math] are said to be orthogonal, denoted [math]\displaystyle{ e\downarrow m }[/math], if for every pair of morphisms [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] such that [math]\displaystyle{ ve=mu }[/math] there is a unique morphism [math]\displaystyle{ w }[/math] such that the diagram
commutes. This notion can be extended to define the orthogonals of sets of morphisms by
- [math]\displaystyle{ H^\uparrow=\{e\quad|\quad\forall h\in H, e\downarrow h\} }[/math] and [math]\displaystyle{ H^\downarrow=\{m\quad|\quad\forall h\in H, h\downarrow m\}. }[/math]
Since in a factorization system [math]\displaystyle{ E\cap M }[/math] contains all the isomorphisms, the condition (3) of the definition is equivalent to
- (3') [math]\displaystyle{ E\subseteq M^\uparrow }[/math] and [math]\displaystyle{ M\subseteq E^\downarrow. }[/math]
Proof: In the previous diagram (3), take [math]\displaystyle{ m:= id ,\ e' := id }[/math] (identity on the appropriate object) and [math]\displaystyle{ m' := m }[/math].
Equivalent definition
The pair [math]\displaystyle{ (E,M) }[/math] of classes of morphisms of C is a factorization system if and only if it satisfies the following conditions:
- Every morphism f of C can be factored as [math]\displaystyle{ f=m\circ e }[/math] with [math]\displaystyle{ e\in E }[/math] and [math]\displaystyle{ m\in M. }[/math]
- [math]\displaystyle{ E=M^\uparrow }[/math] and [math]\displaystyle{ M=E^\downarrow. }[/math]
Weak factorization systems
Suppose e and m are two morphisms in a category C. Then e has the left lifting property with respect to m (respectively m has the right lifting property with respect to e) when for every pair of morphisms u and v such that ve = mu there is a morphism w such that the following diagram commutes. The difference with orthogonality is that w is not necessarily unique.
A weak factorization system (E, M) for a category C consists of two classes of morphisms E and M of C such that:[1]
- The class E is exactly the class of morphisms having the left lifting property with respect to each morphism in M.
- The class M is exactly the class of morphisms having the right lifting property with respect to each morphism in E.
- Every morphism f of C can be factored as [math]\displaystyle{ f=m\circ e }[/math] for some morphisms [math]\displaystyle{ e\in E }[/math] and [math]\displaystyle{ m\in M }[/math].
This notion leads to a succinct definition of model categories: a model category is a pair consisting of a category C and classes of (so-called) weak equivalences W, fibrations F and cofibrations C so that
- C has all limits and colimits,
- [math]\displaystyle{ (C \cap W, F) }[/math] is a weak factorization system,
- [math]\displaystyle{ (C, F \cap W) }[/math] is a weak factorization system, and
- [math]\displaystyle{ W }[/math] satisfies the two-out-of-three property: if [math]\displaystyle{ f }[/math] and [math]\displaystyle{ g }[/math] are composable morphisms and two of [math]\displaystyle{ f,g,g\circ f }[/math] are in [math]\displaystyle{ W }[/math], then so is the third.[2]
A model category is a complete and cocomplete category equipped with a model structure. A map is called a trivial fibration if it belongs to [math]\displaystyle{ F\cap W, }[/math] and it is called a trivial cofibration if it belongs to [math]\displaystyle{ C\cap W. }[/math] An object [math]\displaystyle{ X }[/math] is called fibrant if the morphism [math]\displaystyle{ X\rightarrow 1 }[/math] to the terminal object is a fibration, and it is called cofibrant if the morphism [math]\displaystyle{ 0\rightarrow X }[/math] from the initial object is a cofibration.[3]
References
- Peter Freyd, Max Kelly (1972). "Categories of Continuous Functors I". Journal of Pure and Applied Algebra 2.
- Riehl, Emily (2014), Categorical homotopy theory, Cambridge University Press, doi:10.1017/CBO9781107261457, ISBN 978-1-107-04845-4
External links
- Riehl, Emily (2008), Factorization Systems, http://www.math.jhu.edu/~eriehl/factorization.pdf
 |