Fermat cubic

File:3D model of Fermat cubic.stl In geometry, the Fermat cubic, named after Pierre de Fermat, is a surface defined by

[math]\displaystyle{ x^3 + y^3 + z^3 = 1. \ }[/math]

Methods of algebraic geometry provide the following parameterization of Fermat's cubic:

[math]\displaystyle{ x(s,t) = {3 t - {1\over 3} (s^2 + s t + t^2)^2 \over t (s^2 + s t + t^2) - 3} }[/math]

[math]\displaystyle{ y(s,t) = {3 s + 3 t + {1\over 3} (s^2 + s t + t^2)^2 \over t (s^2 + s t + t^2) - 3} }[/math]

[math]\displaystyle{ z(s,t) = {-3 - (s^2 + s t + t^2) (s + t) \over t (s^2 + s t + t^2) - 3}. }[/math]

In projective space the Fermat cubic is given by

[math]\displaystyle{ w^3+x^3+y^3+z^3=0. }[/math]

The 27 lines lying on the Fermat cubic are easy to describe explicitly: they are the 9 lines of the form (w : aw : y : by) where a and b are fixed numbers with cube −1, and their 18 conjugates under permutations of coordinates.

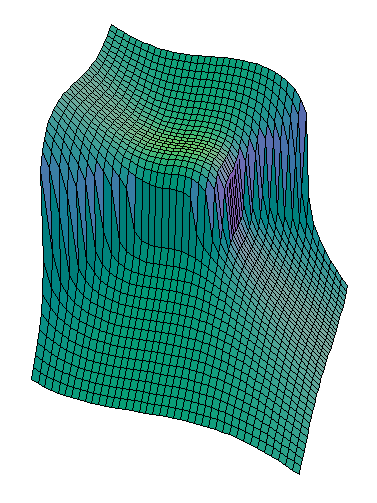
Real points of Fermat cubic surface.

References

• Ness, Linda (1978), "Curvature on the Fermat cubic", Duke Mathematical Journal 45 (4): 797–807, doi:10.1215/s0012-7094-78-04537-4, ISSN 0012-7094, https://projecteuclid.org/euclid.dmj/1077313099 
• Elkies, Noam. "Complete cubic parameterization of the Fermat cubic surface". http://www.math.harvard.edu/~elkies/4cubes.html.