Finance:Balances Mechanics

From HandWiki
Short description: Economic model

The Balances Mechanics (German: Saldenmechanik; from balances of bookkeeping respectively the credit system and mechanics to characterize the strict universal identities) is a work and mean of economics, comparable with Stock-Flow Consistent Modelling. Statements of Balances Mechanics are not based on assumptions and preconditions of a model but are of trivial arithmetic nature, usually shaped as equation and universal without restrictions. Balances Mechanics were developed by Wolfgang Stützel and published in his books Paradoxa der Geld- und Konkurrenzwirtschaft (Paradoxes of Competition-Based Monetary Economies) and Volkswirtschaftliche Saldenmechanik (Balances Mechanics of Economics).[1]

With the balances it becomes obvious: a national economy cannot save.[2]

Overview

Balances Mechanics deals with interrelations, the validity of which – contrary to most economics postulates – does not depend on assumptions about human behaviour.[3] Balances Mechanics allows to put these frequently necessary assumptions of economic theories and postulates onto a logic fundament of overall economics thinking (Size Mechanics). Previously false conclusions in pricing theory, theory of money, and trade cycle theory, resulting from single economy thinking (partial sentence) are overcome by a correct micro foundation and introduction of the real existing credit economy to the modeling (global sentence, size mechanics/relational sentence).[4]

For example, from the view of the single economy experience it seems to be absolutely logical that rising expenses of a national economy go along with a rising need for medium of exchange in terms of quantity theory. From the view of Balances Mechanics one recognizes, with regard to the counter entry, that growing expenses in overall economy mean growing revenues as well and that, for instance, at payment lock step there is no correlation at all between overall sales volume and need for medium of exchange.[5]

Beside the mechanics of the real identities, in particular of buy surplus and sales surplus, it is just the insight from Balances Mechanics thinking that shows many issues, which commonly and with levity are viewed as connected, are not connected mechanically at all. Stützel uses the term "problem plaitings" (German: "Problemverschlingungen") when e.g. the equilibrium of the plans for changes of money assets are identified as invalid with the lock step of those changes and the steady state of the overall expenses or the capital stock. Similar applies to Balances Mechanics of – strictly viewed as separated – operations of money assets and operations of medium of exchange, which can only enable a self-consistent clarification of the interrelations between money system and real economy by using a clear distinction.[6]

Balances Mechanics thus uses the interrelations of real identities and reveals serious fallacies of model making from wrongly assumed identities (ex ante equilibrium conditions/ex post identity equations).[7][8]

Basic concepts

Credit Mechanics: 4 Interrelations in payment flows and bank money expansion/destruction/unchangements (by Decker/Goodhart 2021, p. 8).

Bank money creation and Credit Mechanics

Balances Mechanics considers the mechanics of private credit creation and recognizes the credit mechanics, which comes from Otto Pfleiderer and Wilhelm Lautenbach.[9] (Wolfgang Stützel often spoke of the "Lautenbachsche Kreditmechanik").

From the mechanics of giving a loan it becomes obvious: Once a debtor uses its credit entry,[10] which corresponds to a liability, as payment for a purchase at the market, by Balances Mechanics this creates a surplus of the debtors expenses over its revenues. With that the remainder of the economy has a surplus of revenues over expenses.

This business relationship (temporarily) created new fiat money (if the seller does not use the received money to pay back own bank liabilities).[11] and in tendency leads to national economy value added[12] (in a phase of growing economy only).

This relativises common statements by classic theories which claim that so called capital collector locations would loan deposits from savers to debtors. Because the surplus of expenses of a debtor enables additional property to the economy (lowering liabilities, increasing monetary property) it is valid to say [math]\displaystyle{ I =\gt S }[/math], in no case the opposite.[13]

Economic entities, groups and the overall economy

Stützel distinguishes the totality of all economic entities (overall economy) and groups of economic entities. A group is defined as the totality of all economic entities minus at least one economic entity.

  • Group of economic entities < Sum of all economic entities (overall economy)

Thereby a group also can be a single economic entity. Each group has a complementary group, so that the sum of group plus complementary group gives the overall economy.

  • Group + Complementary Group = Overall Economy

Examples for groups are all private households of a national economy or all companies of a national economy. The group of private economic entities (private sector) is the sum of all companies and all private households.
A national economy is a group as well. It is the sum of all economic entities of a nation (following the inland concept, these are all economic entities inside a state territorium; following the inhabitant concept, these are all economic entities of same nationality).
The complementary group to the sector of private households are all not-households (state, companies, foreign countries). The complementary group of a national economy are all other national economies, the foreign country sector.

So groups can be defined as needed and for a certain purpose.

Sentence categories

Three sentences about the relationship of groups and overall economy can be set:

  1. Partial sentences: These are sentences, which are valid for groups and individual economic entities.
  2. Global sentences: These are sentences, which are valid for the totality of all economic entities.
  3. Size Mechanics: Tells under what conditions (the behaviour of the complementary group) statements for groups and single entities are valid (partial sentences).

When a partial sentence is applied to the totality of economic entities then that is a fallacy of composition.

Example:

  1. Partial sentence: A company rises its sales volume when it lowers its prices.
  2. Global sentence: If all companies lower their prices, sales do not change but the price level lowers.
  3. Size mechanics: A company can only rise its sales volume if the complementary group (all other companies) keeps its prices.

This example is an application of the paradox of competition (Konkurrenzparadoxon).

Single economy and overall economy buildup of money assets

For a single economic entity and groups of economic entities the partial sentence is valid, that the entities can rise their net-money assets by surplus of revenues (partial sentence):

  • Revenues – Expenses = ΔNet money assets

Furthermore, it is valid that the expense of an economic entity A is the revenue of an economic entity B:

  • Expense A = Revenue B

A purchase of a good by a customer leads to a revenue to the seller, the wage payment of an employer leads to the revenue of a worker and so on. Because every expense faces a revenue (and every revenue faces an expense) the sum of all expenses must be the sum of all revenues:

  • Sum revenues = Sum expenses

From that the global sentence derives that the aggregate expense-revenue-balance of a closed aggregate economy equals zero (current account/performance record). This is valid for the global economy and closed national economies. Open national economies are groups because they can have a current account balance value. For them the partial sentence is valid that their net money assets can differ from zero. In addition, it is valid that every debt claim of an economic entity corresponds to a liability of an other economic entity, so that the sum of all claims necessarily corresponds to the sum of all liabilities:

  • Sum claims = Sum liabilities

From that comes the global sentence that the aggregate net financial assets of a closed economy (all claims minus all liabilities) necessarily is Zero. The same is valid for changes of claims and liabilities:

  • Sum Δclaims = Sum Δliabilities

Here the Global Sentence is: The totality of economic entities cannot rise or lower their overall net money assets.

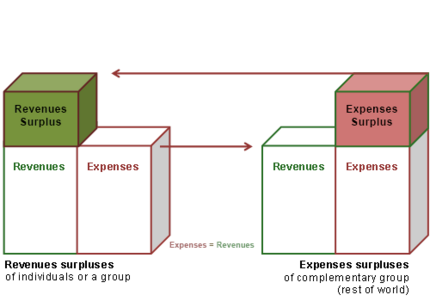
Change of net money assets, because expenses surpluses = revenues surpluses of the complementary group

After all the Size Mechanics shows the conditions which make the partial sentence valid that individuals and groups can change their net money assets by expense-revenue-balances:

  • A group can only rise its net money assets (by surplus of revenue) if its complementary group (the remaining of all economy subjects, literally spoken the rest of the world) lowers its net money assets with the same amount (by an expenses surplus).

Balance of a single economic entity

Every economic entity (individuals, private households, companies, states, national economies etc.) has a balance sheet which consists of assets (activa) and liabilities (passiva). On the assets side there is the tangible assets (examples: machines, buildings, etc.) and the accounts receivable (examples: money, shares, bonds, etc.). On the liabilities side there are the liabilities and the net worth (also called equity).

So it is valid for each economic entity:

  • net worth = tangible assets + claims – liabilities

Claims minus liabilities equals net money assets:

  • net money assets = claims – liabilities

The claims can be divided into medium of exchange and other claims:

  • claims = medium of exchange + other claims

Generally all "other claims" can be converted into a medium of exchange by monetization. Debt claims against business banks are monetized claims because they commonly are accepted as fiat money as medium of exchange.

Application fields

Analysis of money assets streams

The most essential application field of Balances Mechanics in economics is the analysis of changes in net financial assets. Net financial assets is the margin between claims and liabilities and changes with the expense-revenue-balances. In contrast to that, the money creation of the bank system generates medium of exchange against debt (in which an accurate demarcation of medium of exchange as part of the monetary assets is not possible).

Revenue surpluses of a group are only possible if the complementary group enables an expense surplus. Economic relationships always are two-sided, because every expense comes up to a revenue and every debt to a claim. If an economic entity gains more than it spends, the complementary group must spend more than it gains:

  • Revenue surplus of one group = Expense surplus of the complementary group

If individual economic entities cut their expenses, so that their expenses are lower than their revenues the global sentence is as follows:

  • A decline of expenses always leads to a decline of revenues and never to a revenue surplus.[14]

At each economy subject (in the meaning of every individual) revenues and expenses can differ, for all economy subjects (in the meaning of all together) revenues and expenses compulsorily must be equal.[15]

For example, it counts:
Surplus of the private households (financial saving) = expenses surplus of the companies + expenses surplus of the state (state deficit) + expenses surplus of foreign countries (trade balance).

The overall national accounts includes the revenues and expenses surplus (funding balances) of the individual sectors of the national economy (including the foreign sector) and thus it appears: the sum of funding balances of all individual sectors (difference between revenues and expenses) results to Zero.[16]

Action Concurrency and credit demand

Action Concurrency refers to the revenues and expenses balances of a group of agents in any period and describes their similarity in actions at the same time. Stützel defines Action Concurrency as follows:

"Action Concurrency occurs, when - by accidence - the same that applies to the overall economy, applies to individual agents, too" [17]

For example, if revenues would be fully spent (without delay) in favor of other agents and all other agents act the same way (strict revenue-expense concurrency), then the demand for credit of each of the agents would be zero. According to the Size Mechanics theorem, credit demand occurs only if the complementary group generates savings through spending less than is earned:

"Credit demand is a function of the deviation from expenses concurrency, not a function of the level of expenses." [18]

Balances Mechanics and trade cycle theory

Balances Mechanics itself is no trade cycle theory, but it allows the accurate micro founding of the behaviour assumptions needed.

At buyers markets the plans for consumption and investment determine the overall expenses, and with that the overall revenues and the economic cycle. Balances Mechanics allows, with the modeling of the real existing credit economy instead of an imaginary barter economy, to picture the influences of the financial system on the expenses plans.

Balance Mechanics relationships

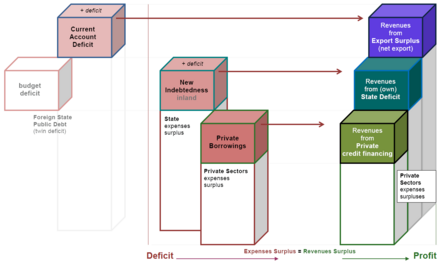
The starting point is the balance of the individual economies' and the state's plans for building monetary assets. If the balance of the plans for building money assets (plans for sales surplus) has a surplus over the plans for money assets reduction (plans for buy surplus) this generates a negative momentum. As a consequence, economic actors overall -as expected- make less expenses in the following periods when they reduce money assets unplanned and make more expenses in the opposite case when their money assets increase by planning.
This momentum is reinforced by the multiplier which results from the average willingness of the economic actors to accept unplanned changes of their money assets.

Wolfgang Stützel describes a theoretical edge case where the state at all costs wants to enforce a buildup of own money assets, but where no private actor wants to accept a reduction of its money assets: "Economy would instantly stand still." He goes on: "In this case the Keynes-multiplier would be negative and of infinite number. Because the sum of plans to heighten money assets would at any revenue level exceed the concurrent plans for reducing money assets."[19]

Balances Mechanics allows from the ex-post-analysis of the funding balances of the macroeconomic accounting (national accounts) as well as from the Balances Mechanics of national debt and in connection with only a few behavioral assumptions, to give very specific policy recommendations in order to limit national debt.

In 2002 Ewald Nowotny for instance explained: "Significant for economy politics thereby is the compulsory Balances Mechanics relationship, that a policy aiming at reducing budget deficits (funding consolidation) can only be successful when it succeeds in reducing the financial surplus of the private households (e.g. by higher private consumption) and/or in rising the debt willingness of companies (for instance, by investments) and/or in improving the trade balance (for example, by additional export)."[20]


See also

References

  1. ↑ Both texts have not been translated into English yet (03/2015). A summary in English is available in Charlotte Bruun's 1995 Dissertation: "Logical Structures and Algorithmic Behavior in A Credit Economy" (online ), Chapter 3: "The Logical Structure of a Monetary Economy", pp. 78-98 (online )
  2. ↑ Wolfgang Waldner, 13. Dezember 2013: flassbeck-economics: Die monetäre Konjunkturtheorie von Keynes:
    "Es existiert ein Widerspruch zwischen dem, was gesamtwirtschaftlich sinnvoll, und dem, was für die Einzelnen vorteilhaft ist. Eine Ökonomie kann kein Geld sparen, jede Einschränkung der Ausgaben führt zum Verlust von Einnahmen." (English: "It exists a contradiction between what is useful for the overall economy and what is beneficial for the individual. An economy cannot save money, every restriction of expenses leads to loss of revenues.")
  3. ↑ Adolf Wagner: Strukturwandel, Arbeitslosigkeit und Veprteilung. Marburg 2003, p. 491.
  4. ↑ Adalbert Winkler: Finanzsystementwicklung, Konsumentenkredite und Wirtschaftswachstum. In: Wolfgang Stützel. Moderne Konzepte für Finanzmärkte, Beschäftigung und Wirtschaftsverfassung. (Hrsg. Schmidt, Ketzel, Prigge) Tübingen 2001, (online auf Google.Books) p. 492-493.
  5. ↑ Wolfgang Stützel: Volkswirtschaftliche Saldenmechanik. Tübingen 2011. p. 232-233.
  6. ↑ Johannes Schmidt: Die Bedeutung der Saldenmechanik für die makroökonomische Theoriebildung. (PDF; 150 kB) p. 6 and following pages
  7. ↑ Michael Frenkel, Klaus Dieter John: Volkswirtschaftliche Gesamtrechnung. München 2011, (online auf Google.Books) p. 30.
  8. ↑ Fritz Voigt (Hrsg.), Wolf-Albright Prautzsch: Die Struktur der Nachfrage von Wirtschaftsunternehmen und privaten Haushalten nach finanziellem Vermögen in der Bundesrepublik Deutschland. Berlin 1971, (online auf Google.Books) p. 33.
  9. ↑ Frank Decker, Charles A.E. Goodhart: Wilhelm Lautenbach’s credit mechanics – a precursor to the current money supply debate, Taylor & Francis, 2021, DOI=10.1080/09672567.2021.1963796.
  10. ↑ Deutsche Bundesbank, 2012: Geld- und Geldpolitik. p. 72: "Geschäftsbanken schaffen Geld durch Kreditvergabe."
  11. ↑ Wilhelm Lautenbach: Zins, Kredit und Produktion. (Hrsg. Wolfgang Stützel) Tübingen 1952. (PDF ) p. 48:
    "Leistet ein Kreditor an einen Debitor, so schrumpft die Kreditsumme, leistet ein Debitor oder einer, der durch die Zahlung Debitor wird, an einen, der nicht Debitor ist, so erhöht sich die Kreditsumme. Sie bleibt aber gleich, wenn ein Debitor an einen anderen Debitor oder ein Kreditor an einen anderen Kreditor leistet." (English: "Remits a creditor to a debtor, the credit sum lowers, remits a debtor or someone who becomes debtor by the payment to someone who is not a debtor, the credit sum rises. But it remains constant when a debtor remits to an other debtor or a creditor remits to an other creditor.")
  12. ↑ Deutsche Bundesbank, 2012: Geld- und Geldpolitik. p. 78:
    "Kreditvergabe und die damit verbundene Geldschöpfung führen deshalb in der Tendenz zu Investitionen und vorgezogenem Konsum und auf diese Weise zu erhöhter Produktion und volkswirtschaftlicher Wertschöpfung." (English: "Credit giving and the corresponding money creation therefore in tendency leads to investment and early consumption and in this way to increased production und national economy value added.")
  13. ↑ Wilhelm Lautenbach: Zins, Kredit und Produktion. (PDF ) p. 34:
    "Um den Gegensatz zur traditionellen Theorie besonders hervortreten zu lassen, kann man den Tatbestand pointiert so ausdrücken: es wird nicht die Investition durch die Ersparnisse, sondern umgekehrt die Ersparnis durch die Investition bestimmt: Die Ersparnis ist ein reiner Verteilungsbegriff. Das Sparen entscheidet nicht über die Gesamtgröße der Investitionen sondern nur über den Anteil der Wirtschaftssubjekte an dem Vermögenszuwachs den die Volkswirtschaft durch die Investition erfährt." (English: "To let the contrast to the traditional theory come forward, the issue can be pithy expressed like this: Saving is a pure term of distribution. Saving does not decide about the total of investments but only about the share which the economic subjects receive from the assets increase that the national economy gains by the investments.")
  14. ↑ Wolfgang Stützel: Volkswirtschaftliche Saldenmechanik Tübingen 2011 p. 76
  15. ↑ Johannes Schmidt: Die Bedeutung der Saldenmechanik für die makroökonomische Theoriebildung. (PDF; 150 kB) p. 3
  16. ↑ Ewald Nowotny: Gründe und Grenzen der öffentlichen Verschuldung. In: Ökonomie in Theorie und Praxis. Berlin und Heidelberg 2002. p. 261.
  17. ↑ Wolfgang Stützel: Volkswirtschaftliche Saldenmechanik. Tübingen 2011. p. 29
  18. ↑ Wolfgang Stützel: Volkswirtschaftliche Saldenmechanik. Tübingen 2011. p. 73 sowie Fußnote auf p. 74, wo Stützel E. Lundberg und B. Senneby zitiert: Das Dilemma der neuen Geldpolitik. (Vierteljahresbericht der Skinddaviska Banken III/1956, Stockholm)
  19. ↑ Wolfgang Stützel: Volkswirtschaftliche Saldenmechanik. Tübingen 2011. p. 86.
  20. ↑ Ewald Nowotny: Gründe und Grenzen der öffentlichen Verschuldung. In: Ökonomie in Theorie und Praxis. Berlin und Heidelberg 2002. p. 261. (online)

Literature

  • Wolfgang Stützel: Volkswirtschaftliche Saldenmechanik. Ein Beitrag zur Geldtheorie. Mohr (Siebeck). Tübingen 1958, Nachdruck der 2. Auflage. Tübingen 2011. (preview at google books) ISBN:978-3161509551
  • Wolfgang Stützel: Paradoxa der Geld- und Konkurrenzwirtschaft. Scientia. Aalen 1979. ISBN:978-3511090296
  • Fabian Lindner: Saving does not Finance Investment. Accounting as an Indispensable Tool for Economic Theory. IMK Working Paper 100, October 2012. Düsseldorf: Macroeconomic Policy Institute (download)
  • Johannes Schmidt: Reforming the Undergraduate Macroeconomics Curriculum: The Case for a Thorough Treatment of Accounting Relationships. Discussion Paper 2/2016, Faculty of Management Science and Engineering. Karlsruhe: Hochschule Technik und Wirtschaft (download)
  • Wolfgang Theil: Systematic Legal Foundations for Monetary Economics. Working Paper presented at WINIR Symposium on Property Rights, April 2016, Bristol UK (download) - last section connects law and accounting to Stützel's mechanics of balances.

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Finance:Balances_Mechanics&oldid=2957939"