Finance:Elasticity of intertemporal substitution
In economics, elasticity of intertemporal substitution (or intertemporal elasticity of substitution, EIS, IES) is a measure of responsiveness of the growth rate of consumption to the real interest rate.[1] If the real interest rate rises, current consumption may decrease due to increased return on savings; but current consumption may also increase as the household decides to consume more immediately, as it is feeling richer. The net effect on current consumption is the elasticity of intertemporal substitution.[2]
Mathematical definition
There are in general two ways to define the EIS. The first way is to define it abstractly as a function derived from the utility function, then interpret it as an elasticity. The second way is to explicitly derive it as an elasticity. The two ways generally yield the same definition.
Abstract definition
Given a utility function [math]\displaystyle{ u(c) }[/math], where [math]\displaystyle{ c }[/math] denotes consumption level, the EIS is defined as[math]\displaystyle{ \sigma(c) = -\frac{u'(c)}{cu''(c)} }[/math]Notice that this definition is the inverse of relative risk aversion.
We can define a family of utility functions, which may be understood as inverse CRRA utility:[math]\displaystyle{ u_\sigma(c) = \begin{cases} \frac{\sigma}{\sigma-1} (c^{\frac{\sigma-1}{\sigma}} - 1) \text{ if } \sigma \neq 1\\ \ln c \quad \text{if }\sigma = 1 \end{cases} }[/math]
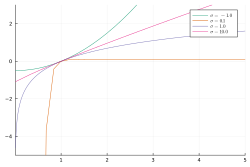
For each [math]\displaystyle{ \sigma \neq 0 }[/math], the utility function [math]\displaystyle{ u_\sigma }[/math] has constant EIS [math]\displaystyle{ \sigma }[/math]. In usual economic applications, there is restriction [math]\displaystyle{ \sigma \gt 0 }[/math], since agents are assumed to not be risk-loving.
In the diagram, one can see that as [math]\displaystyle{ \sigma \to \infty }[/math], the utility curve becomes more linear, indicating that the agent does not attempt to smooth consumption over time, similar to how a risk-neutral agent does not prefer gambles with smoother outcomes.
Derived definition
The derivation differs for discrete and continuous time. We will see that for CRRA utility, the two approaches yield the same answer. The below functional forms assume that utility from consumption is time additively separable.
Discrete time
Total lifetime utility is given by
- [math]\displaystyle{ U=\sum_{t=0}^{T}\beta^{t}u(c_t) }[/math]
In this setting, the gross real interest rate [math]\displaystyle{ R }[/math] will be given by the following condition:
- [math]\displaystyle{ Qu'(c_t) = Q\beta Ru'(c_{t+1}) }[/math]
A quantity of money [math]\displaystyle{ Q }[/math] invested today costs [math]\displaystyle{ Qu'(c_t) }[/math] units of utility, and so must yield exactly that number of units of utility in the future when saved at the prevailing gross interest rate [math]\displaystyle{ R=1+r }[/math], where [math]\displaystyle{ r }[/math] is the net interest rate (if it yielded more, then the agent could make himself better off by saving more).
Solving for the gross interest rate, we see that
- [math]\displaystyle{ R = \frac{u'(c_{t})}{\beta u'(c_{t+1})} }[/math]
In logs, we have
- [math]\displaystyle{ \ln(R) = \ln(1+r) = -\ln{\left[\frac{u'(c_{t+1})}{u'(c_{t})}\right]} - \ln{\beta} }[/math]
Since [math]\displaystyle{ \ln(1+r) \approx r }[/math] for small [math]\displaystyle{ r }[/math] (logs are very close to percentage changes) we have
- [math]\displaystyle{ r \approx -\ln{\left[\frac{u'(c_{t+1})}{u'(c_{t})}\right]} - \ln{\beta} }[/math]
The elasticity of intertemporal substitution is defined as the percent change in consumption growth per percent increase in the net interest rate:
- [math]\displaystyle{ \frac{d\ln(c_{t+1}/c_t)}{d r} }[/math]
By substituting in our log equation above, we can see that this definition is equivalent to the elasticity of consumption growth with respect to marginal utility growth:
- [math]\displaystyle{ -\frac{d\ln(c_{t+1}/c_t)}{d\ln(u'(c_{t+1})/u'(c_t))} }[/math]
Either definition is correct, however, assuming that the agent is optimizing and has time separable utility.
Example
Let utility of consumption in period [math]\displaystyle{ t }[/math] be given by
- [math]\displaystyle{ u(c_t)=\frac{c_t^{1-\sigma}}{1-\sigma}. }[/math]
Since this utility function belongs to the family of CRRA utility functions we have [math]\displaystyle{ u'(c_t)=c_t^{-\sigma}. }[/math] Thus,
- [math]\displaystyle{ \ln\left[\frac{u'(c_{t+1})}{u'(c_t)}\right]=-\sigma\ln\left[\frac{c_{t+1}}{c_t}\right]. }[/math]
This can be rewritten as
- [math]\displaystyle{ \ln\left[\frac{c_{t+1}}{c_t}\right]=-\frac{1}{\sigma}\ln\left[\frac{u'(c_{t+1})}{u'(c_t)}\right] }[/math]
Hence, applying the above derived formula
- [math]\displaystyle{ -\frac{\partial\ln(c_{t+1}/c_t)}{\partial\ln(u'(c_{t+1})/u'(c_t))}=-\left[-\frac{1}{\sigma}\right]=\frac{1}{\sigma}. }[/math]
Continuous time
Let total lifetime utility be given by
[math]\displaystyle{ U=\int_0^T e^{-\rho t} u(c_t) dt }[/math]
where [math]\displaystyle{ c_t }[/math] is shorthand for [math]\displaystyle{ c(t) }[/math], [math]\displaystyle{ u(c(t)) }[/math] is the utility of consumption in (instant) time t, and [math]\displaystyle{ \rho }[/math] is the time discount rate. First define the measure of relative risk aversion (this is useful even if the model has no uncertainty or risk) as,
- [math]\displaystyle{ RRA=-\frac{d(u'(c_t))}{d(c_t)}\frac{c_t}{u'(c_t)}=-u''(c_t)\frac{c_t}{u'(c_t)} }[/math]
then the elasticity of intertemporal substitution is defined as
[math]\displaystyle{ EIS=-\frac{\partial(\dot{c}_{t}/c_t)}{\partial(\dot{u}'(c_t)/u'(c_t))}=-\frac{\partial(\dot{c}_{t}/c_t)}{\partial(u''(c_t)\dot{c}_{t}/u'(c_t))}=\frac{\partial(\dot{c}_{t}/c_t)}{\partial(RRA\cdot(\dot{c}_{t}/c_t))}=\frac{1}{RRA}=-\frac{u'(c_t)}{u''(c_t)\cdot c_t} }[/math]
If the utility function [math]\displaystyle{ u(c) }[/math] is of the CRRA type:
[math]\displaystyle{ u(c)=\frac {c^{1-\theta}-1} {1-\theta} }[/math] (with special case of [math]\displaystyle{ \theta=1 }[/math] being [math]\displaystyle{ u(c)=\ln(c) }[/math])
then the intertemporal elasticity of substitution is given by [math]\displaystyle{ \frac {1} {\theta} }[/math]. In general, a low value of theta (high intertemporal elasticity) means that consumption growth is very sensitive to changes in the real interest rate. For theta equal to 1, the growth rate of consumption responds one for one to changes in the real interest rate. A high theta implies an insensitive consumption growth.
Ramsey Growth model
In the Ramsey growth model, the elasticity of intertemporal substitution determines the speed of adjustment to the steady state and the behavior of the saving rate during the transition. If the elasticity is high, then large changes in consumption are not very costly to consumers and, as a result, if the real interest rate is high, they will save a large portion of their income. If the elasticity is low, the consumption smoothing motive is very strong and because of this consumers will save a little and consume a lot if the real interest rate is high.
Estimates
Empirical estimates of the elasticity vary. Part of the difficulty stems from the fact that microeconomic studies come to different conclusions than macroeconomic studies, which use aggregate data. A meta-analysis of 169 published studies reports a mean elasticity of 0.5, but also substantial differences across countries.[3]
References
 |