Finance:Engel's law

From HandWiki
Short description: Empirical observation in economics that as income rises, less is spent on food
According to Engel's law, the share of income spent on food decreases, even as total food expenditure rises

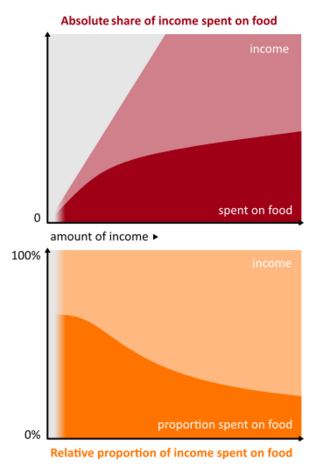
Engel's law is an economic relationship proposed by the statistician Ernst Engel in 1857. It suggests that as family income increases, the percentage spent on food decreases, even though the total amount of food expenditure increases. Expenditure on housing and clothing remains proportionally the same, and that spent on education, health and recreation rises.[1]

Even though Engel's law was proposed roughly 160 years ago, it holds relevance today in the context of poverty, especially the reduction of poverty. For instance, the lines and rates for national poverty are often determined by the food share of household expenditure.[2]

A quotation of Engel himself reveals the same relationship between income and percentage of income spent on food, but also indicates the application of Engel's Law in measuring standard of living:

The poorer is a family, the greater is the proportion of the total outgo [family expenditures] which must be used for food. ...The proportion of the outgo used for food, other things being equal is the best measure of the material standard of living of a population.[2]

Understanding Engel's law

Engel's law states that an increase in the income of a family decreases the proportion of the income which is spent on food, even though the total amount of food expenditure is increasing. In other words, the income elasticity of demand of food is between 0 and 1. For instance, a family with a $5000 monthly income is spending $2000 on food - which is 40%. Say the income of this family would increase by 40% - to $7000. In this case they would spend around $2500 on food. So, although the absolute expenditure on food would increase by 25%, the relative proportion would decrease by 35.7%.[3] This example clearly shows the notion supported by Engel's Law, which is that households with lower income will spend a larger amount of their income on food items than the ones in the middle- or higher-income levels. For a poor family, the budget expenditure is a big portion of their total budget, while the rich tend to spend more of their money on items such as entertainment and luxury goods. To be clear, Engel's law does not imply that food spending remains unchanged as income increases; instead, it suggests that consumers increase their expenditures for food products in percentage terms less than their increases in income. [4][5] The interaction between Engel's law, technological progress, and the process of structural change is crucial for explaining long-term economic growth as suggested by Leon,[6] and Pasinetti.[7]

Engel curve

A concept which is based on Engel's law is Engel curve. This curve shows how the spending on a certain good varies by either the proportion or absolute dollar amount. The shape of the curve depends on factors such as age, gender, educational level and which type of good it is visualising. Moving along the curve assumes that these factors are held constant, ceteris paribus, while only income is changed. Logically, when demographic factors change, the Engel curve shifts accordingly. Moreover, Pope (2012) notes that larger families will have higher food consumption, as well as that consumption expenditures change throughout a life cycle, even holding income and other demographic variables are held constant. The share of a budget spent on food rise and then fall during a lifetime, producing an inverted parabola, indicating that expenditures on food as well as total expenditures peak during mid-life.[8]

With income level as the x-axis and expenditures as the y-axis, the Engel curves show upward slopes for normal goods, which have a positive income elasticity of demand. Inferior goods with negative income elasticity, assume negative slopes for their Engel curves. In the case of food, the Engel curve is concave downward with a positive but decreasing slope.[9][8] Engel argues that food is a normal good, yet the share of household's budget spent on food falls as income increases, making food a necessity.[4][8]

Another example of Engel's law

History of Engel's law

In 1857, by using data from several households, Ernst Engel found that household food expenditure and household income are correlating. The relationship between food share of household expenditure and household income was also highly consistent. The income elasticity for food expenditure was inelastic, below 1 (around .86) for each gathered dataset, meaning it is insensitive to price changes.[10]

By 1875 Engel's law had spread across the Atlantic to Europe. There it gained attention and was used by Carroll D. Wright, which did not only argue that food expenditure was the only thing that varied with income, but that in fact clothing, housing and sundries (meaning expenditures that are not frequently incurred, like home improvement items) also varied with income in agreement with Engel’s law.[11]

In 1932 Zimmerman stated that Engel's law had been utilised for other factors than income to food expenditure, which should not be the practice. He states: "It is evident that Engel's law, rigidly interpreted is not true for particular families, for particular times, and under certain circumstances" and "The 'Engel' type of standard of living applies to no more than half of the people of the globe." Zimmerman argues that the reason for this is among other things personal tastes, family size and cultural preferences.[12]

In a review by Houthakker in 1957, the household incomes and elasticities on food, clothing and miscellaneous items are further investigated, by looking at 40 households from 30 countries. The elasticities are found to be similar to Engel's law, not equal. Based on this research, Houthakker claims that "If no data on the expenditure patterns of a country are available at all, one would not be very far astray by putting the partial elasticity at 0.6 with respect to food."[13]

Since then, researches on patterns concerning food expenditure have mainly become empirical using sophisticated statistical models. This is in part made possible due to the ever-increasing amount of data available. It is today quite common to simultaneously analyse how different types of expenditures change along with household income or total expenditure. In the 21st century there have been relatively few cross-national studies of the extent to which Engel's law remain relevant. However, a study by Richard Anker in 2011 showed "convincing evidence [...] that Engel's law continues to be relevant today across countries as well as across households within countries", but he also draws the conclusion that Engel's law today is only sufficiently strong to predict differences in food shares of countries that have large enough differences when it comes to income per capita.[14] It is important to note that currently researchers assume an income elasticity of food being less than 1.0 (but more than 0.0), which further implies that the share of household expenditure on food decreases with rising income.[2][8] Therefore Engel's law is a commonly accepted economic relationship and often referred to in the introductory sections of academic papers.[2][9][13][10][8]

The Problem

The reliability of the conclusions derived from Engel’s law is non-negotiable as his law can be proved empirically as well as theoretically using today’s methods and theorems. References to Engel's law usually involve his tables from his analysis where the correlation between income and food expenditures is highlighted. The table depicts a series of various annual incomes for families in francs ranging from 200 to 3,000 and the respective share spent on food. The percentage drops from 72.96% for the lowest income family to 56.9% to the highest one hence we can clearly see a drop of 16% which was the main basis for Engel’s claim.

However one issue that is worth raising is how he was able to obtain the 29 observations used as the correlation coefficient between the values is relatively high and Engel never mentioned the method he used to come up with the approximations. One potential method could have been the least-squares estimation which, after coming up with the regression line and applying the adequate coefficients of interpolation, would fit the equation perfectly. Unfortunately, the first known publication of the method was over 30 years after Engel’s paper.

A way simpler possibility comes to mind and it is just drawing a straight line between two points and coming up with all the relevant data graphically. However, even though it is clearly seen in the paper that the income perceived is rising by 100 francs per sample family, the food expenditure is definitely not decreasing following any fixed arithmetic trend but it could be a geometric rate.

His data could have been derived from an approximation following several news articles at the time. For example, a study showed that the average skilled worker in Manchester spent 60% of his earnings on food while a corresponding family would earn around 1,700 annually which is relatively close to Engel’s estimation of 59.79. Several other sources can be quoted which make Engel’s data look more and more reliable. Engel’s data could have either been extracted from a variety of news articles and local studies from the English market at the time or from an approximation that he came up with but the soundness of the conclusion derived from the set is very rational.[15]

Implication today

Engel's law can be used as an indicator when looking at standards of living in various countries. For that purpose a measure called Engel coefficient is used, which is simply a food budget share at a point in time.[8] A country that would be poor and have a lower standard of living would have a high Engel coefficient, whereas a country with higher standards of living would have a lower Engel coefficient. The Engel coefficient is used for this purpose by United Nations , where a coefficient above 59% represents poverty, 50-59% represents a state where daily needs are barely met, 40-50% a moderately well-off standard of living, 30-40% a good standard of living and below 30% a wealthy life.[16]

Inferring well-being from budget share for food. Based on Engel's empirical findings that the share of budget spent on food falls with rising income, suggests that economic growth (and with it rising incomes in the population) is a solution to malnourishment.[8] Using the Engel coefficient countries can set national poverty lines,[2] where the most common measure is to divide the cost of a nutritious diet by the Engel coefficient.[8] In his paper Pope (2012) illustrates that convergence between food budget shares between rural and urban regions have been used to reflect standards of living.[8]

Food's budget share as indicator of changes in real income. Hamilton (2001) interprets Engel's law and suggests that movements in the percentage of budget share spent on food may serve as an indicator of changes to the real income. In his paper, Hamilton (2001) measures the inconsistency of the real income inferred from changes to food budget shares with the real income measured directly and proceeds to estimate the bias in CPI.[17] Food functions as a good indicator of inflation as its income elasticity is sufficiently different from 1.0; food is not durable, implying that expenditure on food is essentially equal to consumption; food is easy to separate from other goods in consumers' utility functions, and lastly food is a good easy to define.[17]

Agricultural sector shrinks as a percentage of total economic activity as a country grows. Engel's law implies that when a country grows, the agricultural sector will constitute a smaller percentage of the country's economic activity. This is due to the fact that the share of income spent on food decreases as income itself increases (from economic growth).[8] Poper (2012) illustrates on the U.S. that the share of workers in the agricultural sector fell from 41% in 1900 to less than 2% in 2000.[8] This phenomenon is reflected in the fact that more developed economies have lesser proportion of the workforce in the agriculutral sector.[8]

Increases in agricultural prices affect the poor disproportionately. From the Engel's law it is evident that food constitutes a large proportion of the budget of the poor, and therefore changes in related prices have a larger impact on the poor than on the rich.[8] Policies which raise agricultural prices will reduce real incomes of the poor proportionately more than they will reduce the incomes of the rich.

See also

References

  1. ↑ "Engel's law". https://www.merriam-webster.com/dictionary/Engel%27s%20law. 
  2. ↑ 2.0 2.1 2.2 2.3 2.4 Anker, R (2011). "Engel's Law Around the World 150 Years Later (PDF)". Political Economy Research Institute 247. https://www.peri.umass.edu/fileadmin/pdf/working_papers/working_papers_201-250/WP247.pdf. Retrieved 2021-03-21. 
  3. ↑ "Engel's Law". 2021. https://corporatefinanceinstitute.com/resources/knowledge/economics/engels-law/. 
  4. ↑ 4.0 4.1 Engel, Ernst (1857). "Die Productions- und Consumtionsverhältnisse des Königreichs Sachsen". Zeitschrift des statistischen Bureaus des Königlich Sächsischen Ministerium des Inneren 8–9: 28–29. "... je aermer eine Familie ist, einen desto groesseren Antheil von der Gesamtausgabe muss zur Beschaffung der Nahrung aufgewendet werden ...". 
  5. ↑ See Timmer, C. P.; Falcon, W. P.; Pearson, S. R. (1983). Food policy Analysis. Baltimore: Johns Hopkins University Press. p. 43. ISBN 0-8018-3072-9. https://archive.org/details/foodpolicyanalys0000timm/page/43. 
  6. ↑ Leon, P. (1967). Structural Change and Growth in Capitalism. Baltimore: Johns Hopkins. https://archive.org/details/structuralchange0000leon. 
  7. ↑ Pasinetti, L (1981). Structural Change and Economic Growth: a Theoretical essay on the dynamics of the wealth of nations. Cambridge University Press. ISBN 0-521-23607-X. https://archive.org/details/structuralchange0000pasi. 
  8. ↑ 8.00 8.01 8.02 8.03 8.04 8.05 8.06 8.07 8.08 8.09 8.10 8.11 8.12 Pope, Rulon (2012). "Engel's Law". BYU Studies Quarterly 51 (3): 119–140. ISSN 2167-8472. https://www.jstor.org/stable/43039896. 
  9. ↑ 9.0 9.1 Chai, A; Moneta, A (2010). "Retrospectives: Engel Curves". Journal of Economic Perspectives 24 (1): 225–240. doi:10.1257/jep.24.1.225. https://www.iris.sssup.it/retrieve/handle/11382/347390/19362/9_ChaiMoneta10.pdf. Retrieved 2021-03-21. 
  10. ↑ 10.0 10.1 Perthel, D (1975). "Engel's law revisited". International Statistical Review 43 (2): 211–218. doi:10.2307/1402900. https://are.berkeley.edu/courses/ARE251/fall2009/Papers/perthel75.pdf. Retrieved 2021-03-21. 
  11. ↑ Wright, C.D (1989). "Prices and Cost of Living. Reprint of 16th Annual Report of the Massachusetts Bureau of Statistics and Labor for 1885.". Wright and Potter Printing. https://www.iris.sssup.it/retrieve/handle/11382/347390/19362/9_ChaiMoneta10.pdf. Retrieved 2021-03-21. 
  12. ↑ Zimmerman, C (1932). "Ernst Engel's law of expenditures for food". The Quarterly Journal of Economics 47 (1): 78–101. doi:10.2307/1885186. https://academic.oup.com/qje/article-abstract/47/1/78/1928220?redirectedFrom=fulltext. Retrieved 2021-03-21. 
  13. ↑ 13.0 13.1 Houthakker, H.S. (1957). "An international comparison of household expenditure patterns, commemorating the centenary of Engel's law". Econometrica 25 (4): 532–551. doi:10.2307/1905382. https://www.jstor.org/stable/1905382. Retrieved 2021-03-21. 
  14. ↑ Anker, R. (2011). "Engel's Law Around the World 150 Years Later (PDF)". Political Economy Research Institute 247: 201–250. https://www.peri.umass.edu/fileadmin/pdf/working_papers/working_papers_201-250/WP247.pdf. Retrieved 2021-03-21. 
  15. ↑ Perthel, D (August 1975). "Engel's Law Revisited". International Statistical Review / Revue Internationale de Statistique (International Statistical Review) 43 (2): 211–218. doi:10.2307/1402900. https://www.jstor.org/stable/1402900. 
  16. ↑ "Engel's Law Explained". 2016-01-16. https://www.romeconomics.com/engels-law-explained/. 
  17. ↑ 17.0 17.1 Hamilton, Bruce W (2001-06-01). "Using Engel's Law to Estimate CPI Bias" (in en). American Economic Review 91 (3): 619–630. doi:10.1257/aer.91.3.619. ISSN 0002-8282. https://pubs.aeaweb.org/doi/10.1257/aer.91.3.619. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Finance:Engel%27s_law&oldid=3317376"