Finance:Synthetic position

A synthetic short position in the underlying, created using a short call and a long put

A synthetic long position in the underlying, created using a long call and a short put

In finance, a synthetic position is a way to create the payoff of a financial instrument using other financial instruments.

A synthetic position can be created by buying or selling the underlying financial instruments and/or derivatives.

If several instruments which have the same payoff as investing in a share are bought, there is a synthetic underlying position. In a similar way, a synthetic option position can be created.

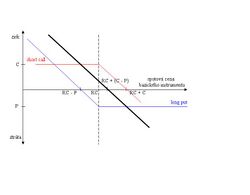
For example, a position which is long a 60-strike call and short a 60-strike put will always result in purchasing the underlying asset for 60 at exercise or expiration. If the underlying asset is above 60, the call is in the money and will be exercised; if the underlying asset is below 60 then the short put position will be assigned, resulting in a (forced) purchase of the underlying at 60.

One advantage of a synthetic position over buying or shorting the underlying stock is that there is no need to borrow the stock if selling it short. Another advantage is that one need not worry about dividend payments on the shorted stock (if any, declared by the underlying security).

When the underlying asset is a stock, a synthetic underlying position is sometimes called a synthetic stock.

Synthetic long put

The synthetic long put position consists of three elements: shorting one stock, holding one European call option and holding [math]\displaystyle{ Ke^{-rT} }[/math] dollars in a bank account.

(Here [math]\displaystyle{ K }[/math] is the strike price of the option, and [math]\displaystyle{ r }[/math] is the continuously compounded interest rate, [math]\displaystyle{ T }[/math] is the time to expiration and [math]\displaystyle{ S }[/math] is the spot price of the stock at option expiration.)

At expiry the stock has to be paid for, which gives a cashflow [math]\displaystyle{ -S }[/math]. The bank account will give a cashflow of [math]\displaystyle{ K }[/math] dollars. Moreover, the European call gives a cashflow of [math]\displaystyle{ \max(0, S-K) }[/math]. The total cashflow is [math]\displaystyle{ K-S+ \max(0,S-K) = \max(0,K-S) }[/math]. The total cashflow at expiry is exactly the cashflow of a European put option.