Four-spiral semigroup
In mathematics, the four-spiral semigroup is a special semigroup generated by four idempotent elements. This special semigroup was first studied by Karl Byleen in a doctoral dissertation submitted to the University of Nebraska in 1977.[1][2] It has several interesting properties: it is one of the most important examples of bi-simple but not completely-simple semigroups;[3] it is also an important example of a fundamental regular semigroup;[2] it is an indispensable building block of bisimple, idempotent-generated regular semigroups.[2] A certain semigroup, called double four-spiral semigroup, generated by five idempotent elements has also been studied along with the four-spiral semigroup.[4][2]
Definition
The four-spiral semigroup, denoted by Sp4, is the free semigroup generated by four elements a, b, c, and d satisfying the following eleven conditions:[2]
- a2 = a, b2 = b, c2 = c, d2 = d.
- ab = b, ba = a, bc = b, cb = c, cd = d, dc = c.
- da = d.
The first set of conditions imply that the elements a, b, c, d are idempotents. The second set of conditions imply that a R b L c R d where R and L are the Green's relations in a semigroup. The lone condition in the third set can be written as d ωl a, where ωl is a biorder relation defined by Nambooripad. The diagram below summarises the various relations among a, b, c, d:
[math]\displaystyle{ \begin{matrix} & & \mathcal{R} & & \\ & a & \longleftrightarrow & b & \\ \omega^l & \Big \uparrow & & \Big \updownarrow & \mathcal{L} \\ & d & \longleftrightarrow & c & \\ & & \mathcal{R} & & \end{matrix} }[/math]
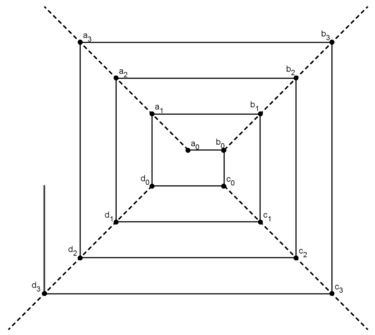
Elements of the four-spiral semigroup
General elements
Every element of Sp4 can be written uniquely in one of the following forms:[2]
- [c] (ac)m [a]
- [d] (bd)n [b]
- [c] (ac)m ad (bd)n [b]
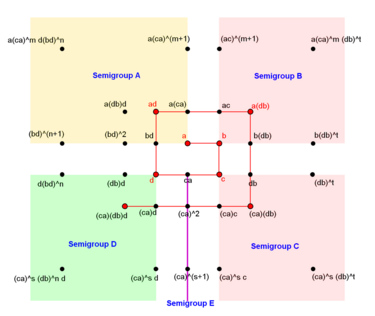
where m and n are non-negative integers and terms in square brackets may be omitted as long as the remaining product is not empty. The forms of these elements imply that Sp4 has a partition Sp4 = A ∪ B ∪ C ∪ D ∪ E where
- A = { a(ca)n, (bd)n+1, a(ca)md(bd)n : m, n non-negative integers }
- B = { (ac)n+1, b(db)n, a(ca)m(db) n+1 : m, n non-negative integers }
- C = { c(ac)m, (db)n+1, (ca)m+1(db)n+1 : m, n non-negative integers }
- D = { d(bd)n, (ca)m+1(db)n+1d : m, n non-negative integers }
- E = { (ca)m : m positive integer }
The sets A, B, C, D are bicyclic semigroups, E is an infinite cyclic semigroup and the subsemigroup D ∪ E is a nonregular semigroup.
Idempotent elements
The set of idempotents of Sp4,[5] is {an, bn, cn, dn : n = 0, 1, 2, ...} where, a0 = a, b0 = b, c0 = c, d0 = d, and for n = 0, 1, 2, ....,
- an+1 = a(ca)n(db)nd
- bn+1 = a(ca)n(db)n+1
- cn+1 = (ca)n+1(db)n+1
- dn+1 = (ca)n+1(db)n+ld
The sets of idempotents in the subsemigroups A, B, C, D (there are no idempotents in the subsemigoup E) are respectively:
- EA = { an : n = 0,1,2, ... }
- EB = { bn : n = 0,1,2, ... }
- EC = { cn : n = 0,1,2, ... }
- ED = { dn : n = 0,1,2, ... }
Four-spiral semigroup as a Rees-matrix semigroup
Let S be the set of all quadruples (r, x, y, s) where r, s, ∈ { 0, 1 } and x and y are nonnegative integers and define a binary operation in S by
[math]\displaystyle{ (r, x, y, s) * (t, z, w, u) = \begin{cases} (r, x-y + \max(y , z + 1), \max(y - 1, z) - z + w, u) & \text{if } s = 0, t = 1\\ (r, x - y+ \max(y, z), \max(y, z) - z + w, u)&\text{otherwise.} \end{cases} }[/math]
The set S with this operation is a Rees matrix semigroup over the bicyclic semigroup, and the four-spiral semigroup Sp4 is isomorphic to S.[2]
Properties
- By definition itself, the four-spiral semigroup is an idempotent generated semigroup (Sp4 is generated by the four idempotents a, b. c, d.)
- The four-spiral semigroup is a fundamental semigroup, that is, the only congruence on Sp4 which is contained in the Green's relation H in Sp4 is the equality relation.
Double four-spiral semigroup
The fundamental double four-spiral semigroup, denoted by DSp4, is the semigroup generated by five elements a, b, c, d, e satisfying the following conditions:[2][4]
- a2 = a, b2 = b, c2 = c, d2 = d, e2 = e
- ab = b, ba = a, bc = b, cb = c, cd = d, dc = c, de = d, ed = e
- ae = e, ea = e
The first set of conditions imply that the elements a, b, c, d, e are idempotents. The second set of conditions state the Green's relations among these idempotents, namely, a R b L c R d L e. The two conditions in the third set imply that e ω a where ω is the biorder relation defined as ω = ωl ∩ ωr.
References
- ↑ Byleen, K. (1977). The Structure of Regular and Inverse Semigroups, Doctoral Dissertation. University of Nebraska.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 Pierre Antoine Grillet (1996). "On the fundamental double four-spiral semigroup". Bulletin of the Belgian Mathematical Society 3: 201 − 208.
- ↑ L.N. Shevrin (originator). "Simple semi-group". Encyclopedia of Mathematics. http://www.encyclopediaofmath.org/index.php?title=Simple_semi-group&oldid=18138. Retrieved 25 January 2014.
- ↑ 4.0 4.1 4.2 Meakin, John; K. Byleen; F. Pastijn (1980). "The double four-spiral semigroup". Simon Stevin 54: 75 & minus 105.
- ↑ Karl Byleen; John Meakin; Francis Pastjin (1978). "The Fundamental Four-Spiral Semigroup". Journal of Algebra 54: 6 − 26. doi:10.1016/0021-8693(78)90018-2.
 |