Fourier operator
The Fourier operator is the kernel of the Fredholm integral of the first kind that defines the continuous Fourier transform, and is a two-dimensional function when it corresponds to the Fourier transform of one-dimensional functions. It is complex-valued and has a constant (typically unity) magnitude everywhere. When depicted, e.g. for teaching purposes, it may be visualized by its separate real and imaginary parts, or as a colour image using a colour wheel to denote phase.[1][2]
It is usually denoted by a capital letter "F" in script font (), e.g. the Fourier transform of a function would be written using the operator as .[3]
It may be thought of as a limiting case for when the size of the discrete Fourier transform increases without bound while its spatial resolution also increases without bound, so as to become both continuous and not necessarily periodic.
Visualization
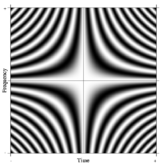
The Fourier operator defines a continuous two-dimensional function that extends along time and frequency axes, outwards to infinity in all four directions. This is analogous to the DFT matrix but, in this case, is continuous and infinite in extent. The value of the function at any point is such that it has the same magnitude everywhere. Along any fixed value of time, the value of the function varies as a complex exponential in frequency. Likewise along any fixed value of frequency the value of the function varies as a complex exponential in time. A portion of the infinite Fourier operator is shown in the illustration below.

Any slice parallel to either of the axes, through the Fourier operator, is a complex exponential, i.e. the real part is a cosine wave and the imaginary part is a sine wave of the same frequency as the real part.
Diagonal slices through the Fourier operator give rise to chirps. Thus rotation of the Fourier operator gives rise to the fractional Fourier transform, which is related to the chirplet transform.[4][5]
See also
References
- ↑ Advances in machine vision: strategies and applications, Colin Archibald and Emil Petriu, ed., Vol. 32, World scientific, . (See the book cover, and pages 99-128, as well as the Preface, page v.)
- ↑ Mann, S. (2018, August). Phenomenological augmented reality with the sequential wave imprinting machine (swim). In 2018 IEEE Games, Entertainment, Media Conference (GEM) (pp. 1-9). IEEE.
- ↑ Coëtmellec, S., Verrier, N., Brunel, M., & Lebrun, D. (2010). General formulation of digital in-line holography from correlation with a chirplet function. Journal of the European Optical Society: Rapid publications, 5, 10027.
- ↑ Millioz, F., & Davies, M. (2012). Sparse detection in the chirplet transform: Application to FMCW radar signals. IEEE Transactions on Signal Processing, 60(6), 2800-2813.
- ↑ Shi, J., Zheng, J., Liu, X., Xiang, W., & Zhang, Q. (2020). Novel Short-Time Fractional Fourier Transform: Theory, Implementation, and Applications. IEEE Transactions on Signal Processing, 68, 3280-3295.
 |