Gammatone filter
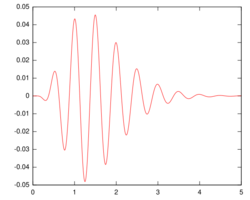
A gammatone filter is a linear filter described by an impulse response that is the product of a gamma distribution and sinusoidal tone. It is a widely used model of auditory filters in the auditory system.
A gammatone response was originally proposed in 1972 as a description of revcor functions measured in the cochlear nucleus of cats.[1]
The gammatone impulse response is given by
- [math]\displaystyle{ g(t) = at^{n-1} e^{-2\pi bt} \cos(2\pi ft + \phi), \, }[/math]
where [math]\displaystyle{ f }[/math] (in Hz) is the center frequency, [math]\displaystyle{ \phi }[/math] (in radians) is the phase of the carrier, [math]\displaystyle{ a }[/math] is the amplitude, [math]\displaystyle{ n }[/math] is the filter's order, [math]\displaystyle{ b }[/math] (in Hz) is the filter's bandwidth,and [math]\displaystyle{ t }[/math] (in seconds) is time.
This time-domain impulse response is a sinusoid (a pure tone) with an amplitude envelope which is a scaled gamma distribution function.[2]
Gammatone filterbank cepstral coefficients (GFCCs) are auditory features that have been used first in the speech domain, and later in the field of underwater target recognition.[citation needed] A bank of gammatone filters is used as an improvement on the triangular filters conventionally used in mel scale filterbanks and MFCC features.
Different ways of motivating the gammatone filter for auditory processing have been presented by Johannesma,[1] Patterson et al.,[3] Hewitt and Meddis,[4] and Lindeberg and Friberg.[5]
Variations
Variations and improvements of the gammatone model of auditory filtering include the complex gammatone filter, the gammachirp filter, the all-pole and one-zero gammatone filters, the two-sided gammatone filter, and filter-cascade models, and various level-dependent and dynamically nonlinear versions of these.[6] Lindeberg and Friberg define a new family of generalized gammatone filters.[5]
References
- ↑ 1.0 1.1 P. I. M. Johannesma (1972). "The pre-response stimulus ensemble of neurons in the cochlear nucleus". IPO Symposium on Hearing Theory. Eindhoven, the Netherlands: pp. 58–69.
- ↑ Slaney, Malcolm (1993). "An Efficient Implementation of the Patterson–Holdsworth Auditory Filter Bank". Apple Computer Technical Report #35. http://rvl4.ecn.purdue.edu/%7Emalcolm/apple/tr35/PattersonsEar.pdf.
- ↑ R. D. Patterson, I. Nimmo-Smith, J. Holdsworth and P. Rice (1987). "An efficient auditory filterbank based on the gammatone function". A Meeting of the IOC Speech Group on Auditory Modelling at RSRE 2 (7).
- ↑ M. J. Hewitt and R. Meddis (1994). "A computer model of amplitude-modulation sensitivity of single units in the inferior colliculus". The Journal of the Acoustical Society of America 95 (4): 2145–2159. doi:10.1121/1.408676. PMID 8201111. Bibcode: 1994ASAJ...95.2145H.
- ↑ 5.0 5.1 T. Lindeberg and A. Friberg (2015). "Idealized computational models for auditory receptive fields". PLOS ONE 10 (3): e0119032. doi:10.1371/journal.pone.0119032. PMID 25822973. Bibcode: 2015PLoSO..1019032L.
- ↑ "History and Future of Auditory Filter Models". Proc. ISCAS. 2010. http://research.google.com/pubs/archive/36895.pdf.
External links
- Slaney's implementation in Mathematica
- Cooke's implementation in C
- A real-time implementation in C++ (for PureData)
- Ellis's "Gammatone-like spectrogram" in Matlab
 |  |
