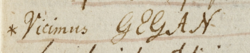Gauss's diary

Short description: Diary of Carl F. Gauss's mathematical discoveries

Gauss's diary was a record of the mathematical discoveries of German mathematician Carl Friedrich Gauss from 1796 to 1814. It was rediscovered in 1897 and published by (Klein 1903), and reprinted in volume X₁ of his collected works and in (Gauss 2005). There is an English translation with commentary given by (Gray 1984), reprinted in the second edition of (Dunnington 2004).

Sample entries

Gauss's first diary entry related to the regular 17-gon (1796)

Gauss's diary entry related to sum of triangular numbers (1796)

Most of the entries consist of a brief and sometimes cryptic statement of a result in Latin.

Entry 1, dated 1796, March 30, states "Principia quibus innititur sectio circuli, ac divisibilitas eiusdem geometrica in septemdecim partes etc.", which records Gauss's discovery of the construction of a heptadecagon by ruler and compass.

Entry 18, dated 1796, July 10, states "ΕΥΡΗΚΑ! num = Δ + Δ + Δ" and records his discovery of a proof that any number is the sum of 3 triangular numbers, a special case of the Fermat polygonal number theorem.

Gauss's diary entry, Vicimus GEGAN

Entry 43, dated 1796, October 21, states "Vicimus GEGAN" (We have conquered GEGAN). The meaning of this was a mystery for many years. (Biermann 1997) found a manuscript by Gauss suggesting that GEGAN is a reversal of the acronym NAGEG standing for Nexum medii Arithmetico-Geometricum Expectationibus Generalibus and refers to the connection between the arithmetic geometric mean and elliptic functions.

Entry 146, dated 1814 July 9, is the last entry, and records an observation relating biquadratic residues and the lemniscate functions, later proved by Gauss and by (Chowla 1940). More precisely, Gauss observed that if a+bi is a (Gaussian) prime and a–1+bi is divisible by 2+2i, then the number of solutions to the congruence 1=xx+yy+xxyy (mod a+bi), including x=∞, y=±i and x=±i, y=∞, is (a–1)²+b².

References

• Gauss, Carl Friedrich. Mathematisches Tagebuch (Ansetzungssachtitel von Bearbeiter/in), Braunschweig, 30.3.1796 - 9.7.1814. Göttinger Digitalisierungszentrum. https://gdz.sub.uni-goettingen.de/id/DE-611-HS-3382323. Retrieved October 8, 2021. 
• Biermann, Kurt-R. (1997), "Vicimus NAGEG. Bestätigung einer Hypothese" (in German), Mitt., Gauß-Ges. Gött. 34: 31–34 
• Chowla, S. (1940), "The last entry in Gauss's diary", Proceedings of the National Academy of Sciences of the United States of America 35 (5): 244–246, doi:10.1073/pnas.35.5.244, ISSN 0027-8424, PMID 16578315 
• Dunnington, G. Waldo (2004), Gray, Jeremy; Dohse, Fritz-Egbert, eds., Carl Friedrich Gauss: Titan of Science, MAA spectrum (2 ed.), Mathematical Association of America, ISBN 9780883855478 
• Gauss, Carl Friedrich (2005), Biermann, Kurt-R., ed., Mathematisches Tagebuch, 1796–1814, Ostwalds Klassiker der exakten Wissenschaften, 256 (Fifth ed.), Frankfurt am Main: Verlag Harri Deutsch, ISBN 978-3-8171-3402-1 
• Gray, J. J. (1984), "A commentary on Gauss's mathematical diary, 1796–1814, with an English translation", Expositiones Mathematicae 2 (2): 97–130, ISSN 0723-0869 
• Klein, Felix (1903), "Gauß' wissenschaftliches Tagebuch 1796–1814", Mathematische Annalen 57: 1–34, doi:10.1007/BF01449013, ISSN 0025-5831, https://zenodo.org/record/2043763