Geometric mean filter

The geometric mean filter is an image filtering process meant to smooth and reduce noise of an image. It is based on the mathematic geometric mean. The output image G(x,y) of a geometric mean is given by

[math]\displaystyle{ G(x,y) = \left[\prod_{i,j\varepsilon S}S(i,j)\right]^{{1\over mn}} }[/math]

Where S(x,y) is the original image, and the filter mask is m by n pixels.

Each pixel of the output image at point (x,y) is given by the product of the pixels within the geometric mean mask raised to the power of 1/mn. For example, using a mask size of 3 by 3, pixel (x,y) in the output image will be the product of S(x,y) and all 8 of its surrounding pixels raised to the 1/9th power.

Using the following original image with pixel (x,y) at the center:

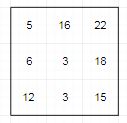Gives the result of: (5*16*22*6*3*18*12*3*15)^(1/9) = 8.77.

Application

The geometric mean filter is most widely used to filter out Gaussian noise. In general it will help smooth the image with less data loss than an arithmetic mean filter.

Code example

The following code shows the application of a geometric mean filter to an image using MATLAB.

% Applies geometric mean filter to image input_noise that has added gaussian noise

[m, n] = size(input_noise);                  
output = zeros(m, n);                       % output image set with placeholder values of all zeros
val = 1;                                    % variable to hold new pixel value

for i = 2:m-2                               % loop through each pixel in original image
    for j = 2:n-2                           % compute geometric mean of 3x3 window around pixel
        p = input_noise(i - 1, j - 1);
        q = input_noise(i - 1, j);
        r = input_noise(i - 1, j + 1);
        s = input_noise(i, j - 1);
        t = input_noise(i, j);
        u = input_noise(i, j + 1);
        v = input_noise(i + 1, j - 1);
        w = input_noise(i + 1, j);
        x = input_noise(i + 1, j + 1);
        
        val = (p * q * r * s * t * u * v * w * x) ^ (1 / 9);
        output(i, j) = val;                 % set output pixel to computed geometric mean
        val = 1;                            % reset val for next pixel
    end
end

File:GMF noise3.tif File:GMF out2.tif