Geospatial topology

From HandWiki
Short description: Type of spatial relationship
Examples of topological spatial relations.

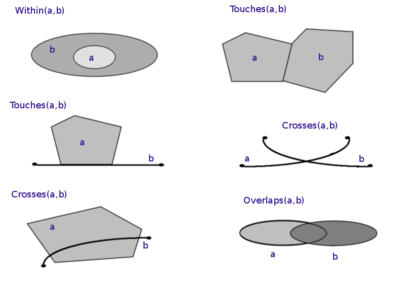
Geospatial topology is the study and application of qualitative spatial relationships between geographic features, or between representations of such features in geographic information, such as in geographic information systems (GIS).[1] For example, the fact that two regions overlap or that one contains the other are examples of topological relationships. It is thus the application of the mathematics of topology to GIS, and is distinct from, but complementary to the many aspects of geographic information that are based on quantitative spatial measurements through coordinate geometry. Topology appears in many aspects of geographic information science and GIS practice, including the discovery of inherent relationships through spatial query, vector overlay and map algebra; the enforcement of expected relationships as validation rules stored in geospatial data; and the use of stored topological relationships in applications such as network analysis.[2][3][4] Spatial topology is the generalization of geospatial topology for non-geographic domains, e.g., CAD software.

Topological relationships

Main page: DE-9IM

In keeping with the definition of topology, a topological relationship between two geographic phenomena is any spatial relation that is not sensitive to measurable aspects of space, including transformations of space (e.g. map projection). Thus, it includes most qualitative spatial relations, such as two features being "adjacent," "overlapping," "disjoint," or one being "within" another; conversely, one feature being "5km from" another, or one feature being "due north of" another are metric relations. One of the first developments of Geographic Information Science in the early 1990s was the work of Max Egenhofer, Eliseo Clementini, Peter di Felice, and others to develop a concise theory of such relations commonly called the 9-Intersection Model, which characterizes the range of topological relationships based on the relationships between the interiors, exteriors, and boundaries of features.[5][6][7][8]

These relationships can also be classified semantically:

  • Inherent relationships are those that are important to the existence or identity of one or both of the related phenomena, such as one expressed in a boundary definition or being a manifestation of a mereological relationship. For example, Nebraska lies within the United States simply because the former was created by the latter as a partition of the territory of the latter. The Missouri River is adjacent to the state of Nebraska because the definition of the boundary of the state says so. These relationships are often stored and enforced in topologically-savvy data.
  • Coincidental relationships are those that are not crucial to the existence of either, although they can be very important. For example, the fact that the Platte River passes through Nebraska is coincidental because both would still exist unproblematically if the relationship did not exist. These relationships are rarely stored as such, but are usually discovered and documented by spatial analysis methods.

Topological data structures and validation

The ARC/INFO Coverage data structure (1981), a topological data model based on POLYVRT

Topology was a very early concern for GIS. The earliest vector systems, such as the Canadian Geographic Information System, did not manage topological relationships, and problems such as sliver polygons proliferated, especially in operations such as vector overlay.[9] In response, topological vector data models were developed, such as GBF/DIME (U.S. Census Bureau, 1967) and POLYVRT (Harvard University, 1976).[10] The strategy of the topological data model is to store topological relationships (primarily adjacency) between features, and use that information to construct more complex features. Nodes (points) are created where lines intersect and are attributed with a list of the connecting lines. Polygons are constructed from any sequence of lines that forms a closed loop. These structures had three advantages over non-topological vector data (often called "spaghetti data"): First, they were efficient (a crucial factor given the storage and processing capacities of the 1970s), because the shared boundary between two adjacent polygons was only stored once; second, they facilitated the enforcement of data integrity by preventing or highlighting topological errors, such as overlapping polygons, dangling nodes (a line not properly connected to other lines), and sliver polygons (small spurious polygons created where two lines should match but do not); and third, they made the algorithms for operations such as vector overlay simpler.[11] Their primary disadvantage was their complexity, being difficult for many users to understand and requiring extra care during data entry. These became the dominant vector data model of the 1980s.

By the 1990s, the combination of cheaper storage and new users who were not concerned with topology led to a resurgence in spaghetti data structures, such as the shapefile. However, the need for stored topological relationships and integrity enforcement still exists. A common approach in current data is to store such as an extended layer on top of data that is not inherently topological. For example, the Esri geodatabase stores vector data ("feature classes") as spaghetti data, but can build a "network dataset" structure of connections on top of a line feature class. The geodatabase can also store a list of topological rules, constraints on topological relationships within and between layers (e.g., counties cannot have gaps, state boundaries must coincide with county boundaries, counties must collectively cover states) that can be validated and corrected.[12] Other systems, such as PostGIS, take a similar approach. A very different approach is to not store topological information in the data at all, but to construct it dynamically, usually during the editing process, to highlight and correct possible errors; this is a feature of GIS software such as ArcGIS Pro and QGIS.[13]

Topology in spatial analysis

Several spatial analysis tools are ultimately based on the discovery of topological relationships between features:

  • spatial query, in which one is searching for the features in one dataset based on desired topological relationships to the features of a second dataset. For example, "where are the student locations within the boundaries of School X?"
  • spatial join, in which the attribute tables of two datasets are combined, with rows being matched based on a desired topological relationship between features in the two datasets, rather than using a stored key as in a normal table join in a relational database. For example, joining the attributes of a schools layer to the table of students based on which school boundary each student resides within.
  • vector overlay, in which two layers (usually polygons) are merged, with new features being created where features from the two input datasets intersect.
  • transport network analysis, a large class of tools in which connected lines (e.g., roads, utility infrastructure, streams) are analyzed using the mathematics of graph theory. The most common example is determining the optimal route between two locations through a street network, as implemented in most street web maps.

Oracle and PostGIS provide fundamental topological operators allowing applications to test for "such relationships as contains, inside, covers, covered by, touch, and overlap with boundaries intersecting."[14][15] Unlike the PostGIS documentation, the Oracle documentation draws a distinction between "topological relationships [which] remain constant when the coordinate space is deformed, such as by twisting or stretching" and "relationships that are not topological [which] include length of, distance between, and area of." These operators are leveraged by applications to ensure that data sets are stored and processed in a topologically correct fashion. However, topological operators are inherently complex and their implementation requires care to be taken with usability and conformance to standards.[16]

See also

  • Digital topology
  • DE-9IM (Dimensionally Extended 9-Intersection Model)

References

  1. ↑ "Topology - GIS Wiki | The GIS Encyclopedia". http://wiki.gis.com/wiki/index.php/Topology#cite_note-3. 
  2. ↑ ESRI White Paper GIS Topology "GIS Topology". ESRI. 2005. http://www.ocw.titech.ac.jp/index.php?module=General&action=DownLoad&file=20142224611080-2-0-1.pdf&type=cal&JWC=20142224611080. 
  3. ↑ Gentle GIS introduction "7. Topology — QGIS Documentation documentation". https://docs.qgis.org/3.16/en/docs/gentle_gis_introduction/topology.html. 
  4. ↑ Ubeda, Thierry; Egenhofer, Max J. (1997). "Topological error correcting in GIS". Advances in Spatial Databases. Lecture Notes in Computer Science. 1262. pp. 281–297. doi:10.1007/3-540-63238-7_35. ISBN 978-3-540-63238-2. 
  5. ↑ Egenhofer, M.J.; Franzosa, R.D. (1991). "Point-set topological spatial relations". Int. J. GIS 5 (2): 161–174. doi:10.1080/02693799108927841. 
  6. ↑ Egenhofer, M.J.; Herring, J.R. (1990). "A Mathematical Framework for the Definition of Topological Relationships". in Brassel, K.. pp. 803–813. http://www.spatial.maine.edu/~max/MJEJRH-SDH1990.pdf. 
  7. ↑ Clementini, Eliseo; Di Felice, Paolino; van Oosterom, Peter (1993). "A small set of formal topological relationships suitable for end-user interaction". in Abel, David; Ooi, Beng Chin. Advances in Spatial Databases: Third International Symposium, SSD '93 Singapore, June 23–25, 1993 Proceedings. Lecture Notes in Computer Science. 692/1993. Springer. pp. 277–295. doi:10.1007/3-540-56869-7_16. ISBN 978-3-540-56869-8. http://resolver.tudelft.nl/uuid:a2db9ae8-f768-4bff-ada3-966a6c8e9db6. 
  8. ↑ Clementini, Eliseo; Sharma, Jayant; Egenhofer, Max J. (1994). "Modelling topological spatial relations: Strategies for query processing". Computers & Graphics 18 (6): 815–822. doi:10.1016/0097-8493(94)90007-8. 
  9. ↑ Goodchild, Michael F. (1977). "Statistical Aspects of the Polygon Overlay Problem". in Dutton, Geoffrey. Harvard Papers in Geographic Information Systems: First International Symposium on Data Structures for Geographic Information Systems. 6: Spatial algorithms. Harvard University. 
  10. ↑ Cooke, Donald F. (1998). "Topology and TIGER: The Census Bureau's Contribution". in Foresman, Timothy W.. The History of Geographic Information Systems: Perspectives from the Pioneers. Prentice Hall. pp. 47–57. 
  11. ↑ Peucker, Thomas K.; Chrisman, Nicholas (1975). "Cartographic Data Structures". The American Cartographer 2 (1): 55–69. doi:10.1559/152304075784447289. 
  12. ↑ "Geodatabase topology". https://pro.arcgis.com/en/pro-app/latest/help/editing/geodatabase-topology.htm. 
  13. ↑ "Topology Checks". OSGEO. https://docs.qgis.org/3.16/en/docs/user_manual/working_with_vector/vector_properties.html#topology-checks. 
  14. ↑ Oracle (2003). "Topology Data Model Overview". Oracle 10g Part No. B10828-01. Oracle. http://docs.oracle.com/html/B10828_01/sdo_topo_concepts.htm#BABDHJAF. 
  15. ↑ "Geometry Relationship Functions". Refractions Research Inc. http://postgis.refractions.net/documentation/manual-1.3/ch06.html#id2574517. 
  16. ↑ Riedemann, Catharina (2004). "Towards Usable Topological Operators at GIS User Interfaces". pp. 669–674. https://agile-online.org/conference_paper/cds/agile_2004/papers/8-1-3_riedemann.pdf. Retrieved 2017-01-11. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Geospatial_topology&oldid=3430275"