Good spanning tree
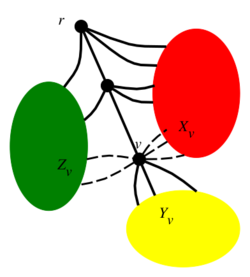
In the mathematical field of graph theory, a good spanning tree [1] [math]\displaystyle{ T }[/math] of an embedded planar graph [math]\displaystyle{ G }[/math] is a rooted spanning tree of [math]\displaystyle{ G }[/math] whose non-tree edges satisfy the following conditions.
- there is no non-tree edge [math]\displaystyle{ (u,v) }[/math] where [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] lie on a path from the root of [math]\displaystyle{ T }[/math] to a leaf,
- the edges incident to a vertex [math]\displaystyle{ v }[/math] can be divided by three sets [math]\displaystyle{ X_v, Y_v }[/math] and [math]\displaystyle{ Z_v }[/math], where,
- [math]\displaystyle{ X_v }[/math] is a set of non-tree edges, they terminate in red zone
- [math]\displaystyle{ Y_v }[/math] is a set of tree edges, they are children of [math]\displaystyle{ v }[/math]
- [math]\displaystyle{ Z_v }[/math] is a set of non-tree edges, they terminate in green zone
Formal definition
Let [math]\displaystyle{ G_\phi }[/math] be a plane graph. Let [math]\displaystyle{ T }[/math] be a rooted spanning tree of [math]\displaystyle{ G_\phi }[/math]. Let [math]\displaystyle{ P(r,v)=(r=u_1), u_2, \ldots, (v=u_k) }[/math] be the path in [math]\displaystyle{ T }[/math] from the root [math]\displaystyle{ r }[/math] to a vertex [math]\displaystyle{ v\ne r }[/math]. The path [math]\displaystyle{ P(r,v) }[/math] divides the children of [math]\displaystyle{ u_i }[/math], [math]\displaystyle{ (1\le i \lt k) }[/math], except [math]\displaystyle{ u_{i+1} }[/math], into two groups; the left group [math]\displaystyle{ L }[/math] and the right group [math]\displaystyle{ R }[/math]. A child [math]\displaystyle{ x }[/math] of [math]\displaystyle{ u_i }[/math] is in group [math]\displaystyle{ L }[/math] and denoted by [math]\displaystyle{ u_{i}^L }[/math] if the edge [math]\displaystyle{ (u_i,x) }[/math] appears before the edge [math]\displaystyle{ (u_i, u_{i+1}) }[/math] in clockwise ordering of the edges incident to [math]\displaystyle{ u_i }[/math] when the ordering is started from the edge [math]\displaystyle{ (u_i,u_{i+1}) }[/math]. Similarly, a child [math]\displaystyle{ x }[/math] of [math]\displaystyle{ u_i }[/math] is in the group [math]\displaystyle{ R }[/math] and denoted by [math]\displaystyle{ u_{i}^R }[/math] if the edge [math]\displaystyle{ (u_i,x) }[/math] appears after the edge [math]\displaystyle{ (u_i, u_{i+1}) }[/math] in clockwise order of the edges incident to [math]\displaystyle{ u_i }[/math] when the ordering is started from the edge [math]\displaystyle{ (u_i,u_{i+1}) }[/math]. The tree [math]\displaystyle{ T }[/math] is called a good spanning tree[1] of [math]\displaystyle{ G_\phi }[/math] if every vertex [math]\displaystyle{ v }[/math] [math]\displaystyle{ (v\ne r) }[/math] of [math]\displaystyle{ G_\phi }[/math] satisfies the following two conditions with respect to [math]\displaystyle{ P(r,v) }[/math].
- [Cond1] [math]\displaystyle{ G_\phi }[/math] does not have a non-tree edge [math]\displaystyle{ (v,u_i) }[/math], [math]\displaystyle{ i\lt k }[/math]; and
- [Cond2] the edges of [math]\displaystyle{ G_\phi }[/math] incident to the vertex [math]\displaystyle{ v }[/math] excluding [math]\displaystyle{ (u_{k-1},v) }[/math] can be partitioned into three disjoint (possibly empty) sets [math]\displaystyle{ X_v,Y_v }[/math] and [math]\displaystyle{ Z_v }[/math] satisfying the following conditions (a)-(c)
- (a) Each of [math]\displaystyle{ X_v }[/math] and [math]\displaystyle{ Z_v }[/math] is a set of consecutive non-tree edges and [math]\displaystyle{ Y_v }[/math] is a set of consecutive tree edges.
- (b) Edges of set [math]\displaystyle{ X_v }[/math], [math]\displaystyle{ Y_v }[/math] and [math]\displaystyle{ Z_v }[/math] appear clockwise in this order from the edge [math]\displaystyle{ (u_{k-1}, v) }[/math].
- (c) For each edge [math]\displaystyle{ (v,v')\in X_v }[/math], [math]\displaystyle{ v' }[/math] is contained in [math]\displaystyle{ T_{u_i^L} }[/math], [math]\displaystyle{ i\lt k }[/math], and for each edge [math]\displaystyle{ (v,v')\in Z_v }[/math], [math]\displaystyle{ v' }[/math] is contained in [math]\displaystyle{ T_{u_i^R} }[/math], [math]\displaystyle{ i\lt k }[/math].
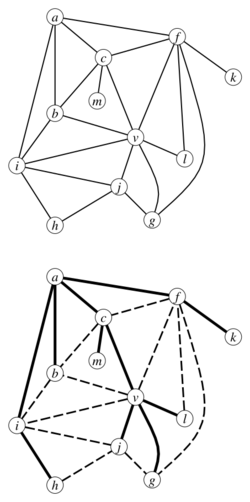
A plane graph [math]\displaystyle{ G_\phi }[/math] (top), a good spanning tree [math]\displaystyle{ T }[/math] of [math]\displaystyle{ G_\phi }[/math] (down) solid edges are part of good spanning tree and dotted edges are non-tree edges in [math]\displaystyle{ G_\phi }[/math] with respect to [math]\displaystyle{ T }[/math].
Applications
In monotone drawing of graphs,[2] in 2-visibility representation of graphs.[1]
Finding good spanning tree
Every planar graph [math]\displaystyle{ G }[/math] has an embedding [math]\displaystyle{ G_\phi }[/math] such that [math]\displaystyle{ G_\phi }[/math] contains a good spanning tree. A good spanning tree and a suitable embedding can be found from [math]\displaystyle{ G }[/math] in linear-time.[1] Not all embeddings of [math]\displaystyle{ G }[/math] contain a good spanning tree.
See also
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Hossain, Md. Iqbal; Rahman, Md. Saidur (23 November 2015). "Good spanning trees in graph drawing". Theoretical Computer Science 607: 149–165. doi:10.1016/j.tcs.2015.09.004.
- ↑ 2.0 2.1 Hossain, Md Iqbal; Rahman, Md Saidur (28 June 2014). "Monotone Grid Drawings of Planar Graphs" (in en). Frontiers in Algorithmics. Lecture Notes in Computer Science. 8497. Springer, Cham. pp. 105–116. doi:10.1007/978-3-319-08016-1_10. ISBN 978-3-319-08015-4.
 |  |
