Graph C*-algebra
In mathematics, a graph C*-algebra is a universal C*-algebra constructed from a directed graph. Graph C*-algebras are direct generalizations of the Cuntz algebras and Cuntz-Krieger algebras, but the class of graph C*-algebras has been shown to also include several other widely studied classes of C*-algebras. As a result, graph C*-algebras provide a common framework for investigating many well-known classes of C*-algebras that were previously studied independently. Among other benefits, this provides a context in which one can formulate theorems that apply simultaneously to all of these subclasses and contain specific results for each subclass as special cases. Although graph C*-algebras include numerous examples, they provide a class of C*-algebras that are surprisingly amenable to study and much more manageable than general C*-algebras. The graph not only determines the associated C*-algebra by specifying relations for generators, it also provides a useful tool for describing and visualizing properties of the C*-algebra. This visual quality has led to graph C*-algebras being referred to as "operator algebras we can see."[1][2] Another advantage of graph C*-algebras is that much of their structure and many of their invariants can be readily computed. Using data coming from the graph, one can determine whether the associated C*-algebra has particular properties, describe the lattice of ideals, and compute K-theoretic invariants.
Graph terminology
The terminology for graphs used by C*-algebraists differs slightly from that used by graph theorists. The term graph is typically taken to mean a directed graph [math]\displaystyle{ E=(E^0, E^1, r, s) }[/math] consisting of a countable set of vertices [math]\displaystyle{ E^0 }[/math], a countable set of edges [math]\displaystyle{ E^1 }[/math], and maps [math]\displaystyle{ r, s : E^1 \rightarrow E^0 }[/math] identifying the range and source of each edge, respectively. A vertex [math]\displaystyle{ v \in E^0 }[/math] is called a sink when [math]\displaystyle{ s^{-1}(v) = \emptyset }[/math]; i.e., there are no edges in [math]\displaystyle{ E }[/math] with source [math]\displaystyle{ v }[/math]. A vertex [math]\displaystyle{ v \in E^0 }[/math] is called an infinite emitter when [math]\displaystyle{ s^{-1}(v) }[/math] is infinite; i.e., there are infinitely many edges in [math]\displaystyle{ E }[/math] with source [math]\displaystyle{ v }[/math]. A vertex is called a singular vertex if it is either a sink or an infinite emitter, and a vertex is called a regular vertex if it is not a singular vertex. Note that a vertex [math]\displaystyle{ v }[/math] is regular if and only if the number of edges in [math]\displaystyle{ E }[/math] with source [math]\displaystyle{ v }[/math] is finite and nonzero. A graph is called row-finite if it has no infinite emitters; i.e., if every vertex is either a regular vertex or a sink.
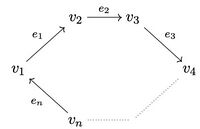
A path is a finite sequence of edges [math]\displaystyle{ e_1 e_2 \ldots e_n }[/math] with [math]\displaystyle{ r(e_i) = s(e_{i+1}) }[/math] for all [math]\displaystyle{ 1 \leq i \leq n-1 }[/math]. An infinite path is a countably infinite sequence of edges [math]\displaystyle{ e_1 e_2 \ldots }[/math] with [math]\displaystyle{ r(e_i) = s(e_{i+1}) }[/math] for all [math]\displaystyle{ i \in \mathbb{N} }[/math]. A cycle is a path [math]\displaystyle{ e_1 e_2 \ldots e_n }[/math] with [math]\displaystyle{ r(e_n) = s(e_1) }[/math], and an exit for a cycle [math]\displaystyle{ e_1 e_2 \ldots e_n }[/math] is an edge [math]\displaystyle{ f \in E^1 }[/math] such that [math]\displaystyle{ s(f) = s(e_i) }[/math] and [math]\displaystyle{ f \neq e_i }[/math] for some [math]\displaystyle{ 1 \leq i \leq n }[/math]. A cycle [math]\displaystyle{ e_1 e_2 \ldots e_n }[/math] is called a simple cycle if [math]\displaystyle{ s(e_i) \neq s(e_1) }[/math] for all [math]\displaystyle{ 2 \leq i \leq n }[/math].
The following are two important graph conditions that arise in the study of graph C*-algebras.
Condition (L): Every cycle in the graph has an exit.
Condition (K): There is no vertex in the graph that is on exactly one simple cycle. Equivalently, a graph satisfies Condition (K) if and only if each vertex in the graph is either on no cycles or on two or more simple cycles.
The Cuntz-Krieger Relations and the Universal Property
A Cuntz-Krieger [math]\displaystyle{ E }[/math]-family is a collection [math]\displaystyle{ \{ s_e, p_v : e \in E^1, v \in E^0 \} }[/math] in a C*-algebra such that the elements of [math]\displaystyle{ \{ s_e : e \in E^1\} }[/math] are partial isometries with mutually orthogonal ranges, the elements of [math]\displaystyle{ \{ p_v : v \in E^0\} }[/math] are mutually orthogonal projections, and the following three relations (called the Cuntz-Krieger relations) are satisfied:
(CK1) [math]\displaystyle{ s_e^*s_e = p_{r(e)} }[/math] for all [math]\displaystyle{ e \in E^1 }[/math],
(CK2) [math]\displaystyle{ p_v = \sum_{s(e)=v} s_e s_e^* }[/math] whenever [math]\displaystyle{ v }[/math] is a regular vertex, and
(CK3) [math]\displaystyle{ s_e s_e^* \le p_{s(e)} }[/math] for all [math]\displaystyle{ e \in E^1 }[/math].
The graph C*-algebra corresponding to [math]\displaystyle{ E }[/math], denoted by [math]\displaystyle{ C^*(E) }[/math], is defined to be the C*-algebra generated by a Cuntz-Krieger [math]\displaystyle{ E }[/math]-family that is universal in the sense that whenever [math]\displaystyle{ \{ t_e, q_v : e \in E^1, v \in E^0 \} }[/math] is a Cuntz-Krieger [math]\displaystyle{ E }[/math]-family in a C*-algebra [math]\displaystyle{ A }[/math] there exists a [math]\displaystyle{ * }[/math]-homomorphism [math]\displaystyle{ \phi : C^*(E) \to A }[/math] with [math]\displaystyle{ \phi(s_e) = t_e }[/math] for all [math]\displaystyle{ e \in E^1 }[/math] and [math]\displaystyle{ \phi(p_v)=q_v }[/math] for all [math]\displaystyle{ v \in E^0 }[/math]. Existence of [math]\displaystyle{ C^*(E) }[/math] for any graph [math]\displaystyle{ E }[/math] was established by Kumjian, Pask, and Raeburn.[3] Uniqueness of [math]\displaystyle{ C^*(E) }[/math] (up to [math]\displaystyle{ * }[/math]-isomorphism) follows directly from the universal property.
Edge Direction Convention
It is important to be aware that there are competing conventions regarding the "direction of the edges" in the Cuntz-Krieger relations. Throughout this article, and in the way that the relations are stated above, we use the convention first established in the seminal papers on graph C*-algebras.[3][4] The alternate convention, which is used in Raeburn's CBMS book on Graph Algebras,[5] interchanges the roles of the range map [math]\displaystyle{ r }[/math] and the source map [math]\displaystyle{ s }[/math] in the Cuntz-Krieger relations. The effect of this change is that the C*-algebra of a graph for one convention is equal to the C*-algebra of the graph with the edges reversed when using the other convention.
Row-Finite Graphs
In the Cuntz-Krieger relations, (CK2) is imposed only on regular vertices. Moreover, if [math]\displaystyle{ v \in E^0 }[/math] is a regular vertex, then (CK2) implies that (CK3) holds at [math]\displaystyle{ v }[/math]. Furthermore, if [math]\displaystyle{ v \in E^0 }[/math] is a sink, then (CK3) vacuously holds at [math]\displaystyle{ v }[/math]. Thus, if [math]\displaystyle{ E }[/math] is a row-finite graph, the relation (CK3) is superfluous and a collection [math]\displaystyle{ \{ s_e, p_v : e \in E^1, v \in E^0 \} }[/math] of partial isometries with mutually orthogonal ranges and mutually orthogonal projections is a Cuntz-Krieger [math]\displaystyle{ E }[/math]-family if and only if the relation in (CK1) holds at all edges in [math]\displaystyle{ E }[/math] and the relation in (CK2) holds at all vertices in [math]\displaystyle{ E }[/math] that are not sinks. The fact that the Cuntz-Krieger relations take a simpler form for row-finite graphs has technical consequences for many results in the subject. Not only are results easier to prove in the row-finite case, but also the statements of theorems are simplified when describing C*-algebras of row-finite graphs. Historically, much of the early work on graph C*-algebras was done exclusively in the row-finite case. Even in modern work, where infinite emitters are allowed and C*-algebras of general graphs are considered, it is common to state the row-finite case of a theorem separately or as a corollary, since results are often more intuitive and transparent in this situation.
Examples
The graph C*-algebra has been computed for many graphs. Conversely, for certain classes of C*-algebras it has been shown how to construct a graph whose C*-algebra is [math]\displaystyle{ * }[/math]-isomorphic or Morita equivalent to a given C*-algebra of that class.
The following table shows a number of directed graphs and their C*-algebras. We use the convention that a double arrow drawn from one vertex to another and labeled [math]\displaystyle{ \infty }[/math] indicates that there are a countably infinite number of edges from the first vertex to the second.
| Directed Graph [math]\displaystyle{ E }[/math] | Graph C*-algebra [math]\displaystyle{ C^*(E) }[/math] |
|---|---|
| [math]\displaystyle{ \mathbb{C} }[/math], the complex numbers | |
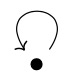 |
[math]\displaystyle{ C(\mathbb{T}) }[/math], the complex-valued continuous functions on the circle [math]\displaystyle{ \mathbb{T} }[/math] |
| [math]\displaystyle{ M_n(\mathbb{C}) }[/math], the [math]\displaystyle{ n \times n }[/math] matrices with entries in [math]\displaystyle{ \mathbb{C} }[/math] | |
| [math]\displaystyle{ \mathcal{K} }[/math], the compact operators on a separable infinite-diemnsional Hilbert space | |
 |
[math]\displaystyle{ M_n(C(\mathbb{T})) }[/math], the [math]\displaystyle{ n \times n }[/math] matrices with entries in [math]\displaystyle{ C(\mathbb{T}) }[/math] |
 |
[math]\displaystyle{ \mathcal{O}_n }[/math], the Cuntz algebra generated by [math]\displaystyle{ n }[/math] isometries |
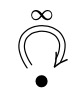 |
[math]\displaystyle{ \mathcal{O}_\infty }[/math], the Cuntz algebra generated by a countably infinite number of isometries |
| [math]\displaystyle{ \mathcal{K}^1 }[/math], the unitization of the algebra of compact operators [math]\displaystyle{ \mathcal{K} }[/math] | |
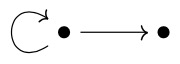 |
[math]\displaystyle{ \mathcal{T} }[/math], the Toeplitz algebra |
The class of graph C*-algebras has been shown to contain various classes of C*-algebras. The C*-algebras in each of the following classes may be realized as graph C*-algebras up to [math]\displaystyle{ * }[/math]-isomorphism:
- Cuntz algebras
- Cuntz-Krieger algebras
- finite-dimensional C*-algebras
- stable AF algebras
The C*-algebras in each of the following classes may be realized as graph C*-algebras up to Morita equivalence:
- AF algebras[6]
- Kirchberg algebras with free K1-group
Correspondence between graph and C*-algebraic properties
One remarkable aspect of graph C*-algebras is that the graph [math]\displaystyle{ E }[/math] not only describes the relations for the generators of [math]\displaystyle{ C^*(E) }[/math], but also various graph-theoretic properties of [math]\displaystyle{ E }[/math] can be shown to be equivalent to C*-algebraic properties of [math]\displaystyle{ C^*(E) }[/math]. Indeed, much of the study of graph C*-algebras is concerned with developing a lexicon for the correspondence between these properties, and establishing theorems of the form "The graph [math]\displaystyle{ E }[/math] has a certain graph-theoretic property if and only if the C*-algebra [math]\displaystyle{ C^*(E) }[/math] has a corresponding C*-algebraic property." The following table provides a short list of some of the more well-known equivalences.
| Property of [math]\displaystyle{ E }[/math] | Property of [math]\displaystyle{ C^*(E) }[/math] |
|---|---|
| [math]\displaystyle{ E }[/math] is a finite graph. | [math]\displaystyle{ C^*(E) }[/math] is finite dimensional. |
| The vertex set [math]\displaystyle{ E^0 }[/math] is finite. | [math]\displaystyle{ C^*(E) }[/math] is unital (i.e., [math]\displaystyle{ C^*(E) }[/math] contains a multiplicative identity). |
| [math]\displaystyle{ E }[/math] has no cycles. | [math]\displaystyle{ C^*(E) }[/math] is an AF algebra. |
[math]\displaystyle{ E }[/math] satisfies the following three properties:
|
[math]\displaystyle{ C^*(E) }[/math] is simple. |
[math]\displaystyle{ E }[/math] satisfies the following three properties:
|
Every hereditary subalgebra of [math]\displaystyle{ C^*(E) }[/math] contains an infinite projection. (When [math]\displaystyle{ C^*(E) }[/math] is simple this is equivalent to [math]\displaystyle{ C^*(E) }[/math] being purely infinite.) |
The gauge action
The universal property produces a natural action of the circle group [math]\displaystyle{ \mathbb{T} := \{ z \in \C : |z| = 1 \} }[/math] on [math]\displaystyle{ C^*(E) }[/math] as follows: If [math]\displaystyle{ \{ s_e, p_v : e \in E^1, v \in E^0 \} }[/math] is a universal Cuntz-Krieger [math]\displaystyle{ E }[/math]-family, then for any unimodular complex number [math]\displaystyle{ z \in \mathbb{T} }[/math], the collection [math]\displaystyle{ \{ zs_e, p_v : e \in E^1, v \in E^0 \} }[/math] is a Cuntz-Krieger [math]\displaystyle{ E }[/math]-family, and the universal property of [math]\displaystyle{ C^*(E) }[/math] implies there exists a [math]\displaystyle{ * }[/math]-homomorphism [math]\displaystyle{ \gamma_z : C^*(E) \to C^*(E) }[/math] with [math]\displaystyle{ \gamma_z (s_e) = zs_e }[/math] for all [math]\displaystyle{ e \in E^1 }[/math] and [math]\displaystyle{ \gamma_z(p_v) = p_v }[/math] for all [math]\displaystyle{ v \in E^0 }[/math]. For each [math]\displaystyle{ z \in \mathbb{T} }[/math] the [math]\displaystyle{ * }[/math]-homomorphism [math]\displaystyle{ \gamma_\overline{z} }[/math] is an inverse for [math]\displaystyle{ \gamma_z }[/math], and thus [math]\displaystyle{ \gamma_z }[/math] is an automorphism. This yields a strongly continuous action [math]\displaystyle{ \gamma: \mathbb{T} \to \operatorname{Aut} C^*(E) }[/math] by defining [math]\displaystyle{ \gamma(z) := \gamma_z }[/math]. The gauge action [math]\displaystyle{ \gamma }[/math] is sometimes called the canonical gauge action on [math]\displaystyle{ C^*(E) }[/math]. It is important to note that the canonical gauge action depends on the choice of the generating Cuntz-Krieger [math]\displaystyle{ E }[/math]-family [math]\displaystyle{ \{ s_e, p_v : e \in E^1, v \in E^0 \} }[/math]. The canonical gauge action is a fundamental tool in the study of [math]\displaystyle{ C^*(E) }[/math]. It appears in statements of theorems, and it is also used behind the scenes as a technical device in proofs.
The uniqueness theorems
There are two well-known uniqueness theorems: the gauge-invariant uniqueness theorem and the Cuntz-Krieger uniqueness theorem. The uniqueness theorems are fundamental results in the study of graph C*-algebras, and they serve as cornerstones of the theory. Each provides sufficient conditions for a [math]\displaystyle{ * }[/math]-homomorphism from [math]\displaystyle{ C^*(E) }[/math] into a C*-algebra to be injective. Consequently, the uniqueness theorems can be used to determine when a C*-algebra generated by a Cuntz-Krieger [math]\displaystyle{ E }[/math]-family is isomorphic to [math]\displaystyle{ C^*(E) }[/math]; in particular, if [math]\displaystyle{ A }[/math] is a C*-algebra generated by a Cuntz-Krieger [math]\displaystyle{ E }[/math]-family, the universal property of [math]\displaystyle{ C^*(E) }[/math] produces a surjective [math]\displaystyle{ * }[/math]-homomorphism [math]\displaystyle{ \phi : C^*(E) \to A }[/math], and the uniqueness theorems each give conditions under which [math]\displaystyle{ \phi }[/math] is injective, and hence an isomorphism. Formal statements of the uniqueness theorems are as follows:
The Gauge-Invariant Uniqueness Theorem: Let [math]\displaystyle{ E }[/math] be a graph, and let [math]\displaystyle{ C^*(E) }[/math] be the associated graph C*-algebra. If [math]\displaystyle{ A }[/math] is a C*-algebra and [math]\displaystyle{ \phi : C^*(E) \to A }[/math] is a [math]\displaystyle{ * }[/math]-homomorphism satisfying the following two conditions:
- there exists a gauge action [math]\displaystyle{ \beta : \mathbb{T} \to \operatorname{Aut} A }[/math] such that [math]\displaystyle{ \phi \circ \beta_z = \gamma_z \circ \phi }[/math] for all [math]\displaystyle{ z \in \mathbb{T} }[/math], where [math]\displaystyle{ \gamma }[/math] denotes the canonical gauge action on [math]\displaystyle{ C^*(E) }[/math], and
- [math]\displaystyle{ \phi(p_v) \neq 0 }[/math] for all [math]\displaystyle{ v \in E^0 }[/math],
then [math]\displaystyle{ \phi }[/math] is injective.
The Cuntz-Krieger Uniqueness Theorem: Let [math]\displaystyle{ E }[/math] be a graph satisfying Condition (L), and let [math]\displaystyle{ C^*(E) }[/math] be the associated graph C*-algebra. If [math]\displaystyle{ A }[/math] is a C*-algebra and [math]\displaystyle{ \phi : C^*(E) \to A }[/math] is a [math]\displaystyle{ * }[/math]-homomorphism with [math]\displaystyle{ \phi(p_v) \neq 0 }[/math] for all [math]\displaystyle{ v \in E^0 }[/math], then [math]\displaystyle{ \phi }[/math] is injective.
The gauge-invariant uniqueness theorem implies that if [math]\displaystyle{ \{ s_e, p_v : e \in E^1, v \in E^0 \} }[/math] is a Cuntz-Krieger [math]\displaystyle{ E }[/math]-family with nonzero projections and there exists a gauge action [math]\displaystyle{ \beta }[/math] with [math]\displaystyle{ \beta_z (p_v) = p_v }[/math] and [math]\displaystyle{ \beta_z (s_e) = zs_e }[/math] for all [math]\displaystyle{ v \in E^0 }[/math], [math]\displaystyle{ e \in E^1 }[/math], and [math]\displaystyle{ z \in \mathbb{T} }[/math], then [math]\displaystyle{ \{ s_e, p_v : e \in E^1, v \in E^0 \} }[/math] generates a C*-algebra isomorphic to [math]\displaystyle{ C^*(E) }[/math]. The Cuntz-Krieger uniqueness theorem shows that when the graph satisfies Condition (L) the existence of the gauge action is unnecessary; if a graph [math]\displaystyle{ E }[/math] satisfies Condition (L), then any Cuntz-Krieger [math]\displaystyle{ E }[/math]-family with nonzero projections generates a C*-algebra isomorphic to [math]\displaystyle{ C^*(E) }[/math].
Ideal structure
The ideal structure of [math]\displaystyle{ C^*(E) }[/math] can be determined from [math]\displaystyle{ E }[/math]. A subset of vertices [math]\displaystyle{ H \subseteq E^0 }[/math] is called hereditary if for all [math]\displaystyle{ e \in E^1 }[/math], [math]\displaystyle{ s(e) \in H }[/math] implies [math]\displaystyle{ r(e) \in H }[/math]. A hereditary subset [math]\displaystyle{ H }[/math] is called saturated if whenever [math]\displaystyle{ v }[/math] is a regular vertex with [math]\displaystyle{ s^{-1}(v) \subseteq H }[/math], then [math]\displaystyle{ v \in H }[/math]. The saturated hereditary subsets of [math]\displaystyle{ E }[/math] are partially ordered by inclusion, and they form a lattice with meet [math]\displaystyle{ H_1 \wedge H_2 := H_1 \cap H_2 }[/math] and join [math]\displaystyle{ H_1 \vee H_2 }[/math] defined to be the smallest saturated hereditary subset containing [math]\displaystyle{ H_1 \cup H_2 }[/math].
If [math]\displaystyle{ H }[/math] is a saturated hereditary subset, [math]\displaystyle{ I_H }[/math] is defined to be closed two-sided ideal in [math]\displaystyle{ C^*(E) }[/math] generated by [math]\displaystyle{ \{ p_v : v \in H \} }[/math]. A closed two-sided ideal [math]\displaystyle{ I }[/math] of [math]\displaystyle{ C^*(E) }[/math] is called gauge invariant if [math]\displaystyle{ \gamma_z(a) \in C^*(E) }[/math] for all [math]\displaystyle{ a \in I }[/math] and [math]\displaystyle{ z \in \mathbb{T} }[/math]. The gauge-invariant ideals are partially ordered by inclusion and form a lattice with meet [math]\displaystyle{ I_1 \wedge I_2 := I_1 \cap I_2 }[/math] and joint [math]\displaystyle{ I_1 \vee I_2 }[/math] defined to be the ideal generated by [math]\displaystyle{ I_1 \cup I_2 }[/math]. For any saturated hereditary subset [math]\displaystyle{ H }[/math], the ideal [math]\displaystyle{ I_H }[/math] is gauge invariant.
The following theorem shows that gauge-invariant ideals correspond to saturated hereditary subsets.
Theorem: Let [math]\displaystyle{ E }[/math] be a row-finite graph. Then the following hold:
- The function [math]\displaystyle{ H \mapsto I_H }[/math] is a lattice isomorphism from the lattice of saturated hereditary subsets of [math]\displaystyle{ E }[/math] onto the lattice of gauge-invariant ideals of [math]\displaystyle{ C^*(E) }[/math] with inverse given by [math]\displaystyle{ I \mapsto \{ v \in E^0 : p_v \in I \} }[/math].
- For any saturated hereditary subset [math]\displaystyle{ H }[/math], the quotient [math]\displaystyle{ C^*(E)/I_H }[/math] is [math]\displaystyle{ * }[/math]-isomorphic to [math]\displaystyle{ C^*(E \setminus H) }[/math], where [math]\displaystyle{ E \setminus H }[/math] is the subgraph of [math]\displaystyle{ E }[/math] with vertex set [math]\displaystyle{ (E \setminus H)^0 := E^0 \setminus H }[/math] and edge set [math]\displaystyle{ (E \setminus H)^1 := E^1 \setminus r^{-1}(H) }[/math].
- For any saturated hereditary subset [math]\displaystyle{ H }[/math], the ideal [math]\displaystyle{ I_H }[/math] is Morita equivalent to [math]\displaystyle{ C^*(E_H) }[/math], where [math]\displaystyle{ E_H }[/math] is the subgraph of [math]\displaystyle{ E }[/math] with vertex set [math]\displaystyle{ E_H^0 := H }[/math] and edge set [math]\displaystyle{ E_H^1 := s^{-1}(H) }[/math].
- If [math]\displaystyle{ E }[/math] satisfies Condition (K), then every ideal of [math]\displaystyle{ C^*(E) }[/math] is gauge invariant, and the ideals of [math]\displaystyle{ C^*(E) }[/math] are in one-to-one correspondence with the saturated hereditary subsets of [math]\displaystyle{ E }[/math].
K-theory
The K-groups of a graph C*-algebra may be computed entirely in terms of information coming from the graph. If [math]\displaystyle{ E }[/math] is a row-finite graph, the vertex matrix of [math]\displaystyle{ E }[/math] is the [math]\displaystyle{ E^0 \times E^0 }[/math] matrix [math]\displaystyle{ A_E }[/math] with entry [math]\displaystyle{ A_E(v,w) }[/math] defined to be the number of edges in [math]\displaystyle{ E }[/math] from [math]\displaystyle{ v }[/math] to [math]\displaystyle{ w }[/math]. Since [math]\displaystyle{ E }[/math] is row-finite, [math]\displaystyle{ A_E }[/math] has entries in [math]\displaystyle{ \mathbb{N} \cup \{ 0 \} }[/math] and each row of [math]\displaystyle{ A_E }[/math] has only finitely many nonzero entries. (In fact, this is where the term "row-finite" comes from.) Consequently, each column of the transpose [math]\displaystyle{ A_E^t }[/math] contains only finitely many nonzero entries, and we obtain a map [math]\displaystyle{ A_E^t : \bigoplus_{E^0} \mathbb{Z} \to \bigoplus_{E^0} \mathbb{Z} }[/math] given by left multiplication. Likewise, if [math]\displaystyle{ I }[/math] denotes the [math]\displaystyle{ E^0 \times E^0 }[/math] identity matrix, then [math]\displaystyle{ I - A_E^t : \bigoplus_{E^0} \mathbb{Z} \to \bigoplus_{E^0} \mathbb{Z} }[/math] provides a map given by left multiplication.
Theorem: Let [math]\displaystyle{ E }[/math] be a row-finite graph with no sinks, and let [math]\displaystyle{ A_E }[/math] denote the vertex matrix of [math]\displaystyle{ E }[/math]. Then
- [math]\displaystyle{ I - A_E^t : \bigoplus_{E^0} \mathbb{Z} \to \bigoplus_{E^0} \mathbb{Z} }[/math]
gives a well-defined map by left multiplication. Furthermore,
- [math]\displaystyle{ K_0(C^*(E)) \cong \operatorname{coker} (I- A_E^t) \qquad \text{and} \qquad K_1(C^*(E)) \cong \operatorname{ker} (I- A_E^t) }[/math].
In addition, if [math]\displaystyle{ C^*(E) }[/math] is unital (or, equivalently, [math]\displaystyle{ E^0 }[/math] is finite), then the isomorphism [math]\displaystyle{ K_0(C^*(E)) \cong \operatorname{coker} (I- A_E^t) }[/math] takes the class of the unit in [math]\displaystyle{ K_0(C^*(E)) }[/math] to the class of the vector [math]\displaystyle{ (1, 1, \ldots, 1) }[/math] in [math]\displaystyle{ \operatorname{coker} (I- A_E^t) }[/math].
Since [math]\displaystyle{ K_1(C^*(E)) }[/math] is isomorphic to a subgroup of the free group [math]\displaystyle{ \bigoplus_{E^0} \mathbb{Z} }[/math], we may conclude that [math]\displaystyle{ K_1(C^*(E)) }[/math] is a free group. It can be shown that in the general case (i.e., when [math]\displaystyle{ E }[/math] is allowed to contain sinks or infinite emitters) that [math]\displaystyle{ K_1(C^*(E)) }[/math] remains a free group. This allows one to produce examples of C*-algebras that are not graph C*-algebras: Any C*-algebra with a non-free K1-group is not Morita equivalent (and hence not isomorphic) to a graph C*-algebra.
Notes
- ↑ 2004 NSF-CBMS Conference on Graph Algebras [1]
- ↑ NSF Award [2]
- ↑ 3.0 3.1 Kumjian, Alex; Pask, David; Raeburn, Iain Cuntz-Krieger algebras of directed graphs. Pacific J. Math. 184 (1998), no. 1, 161–174.
- ↑ Bates, Teresa; Pask, David; Raeburn, Iain; Szymański, Wojciech The C*-algebras of row-finite graphs. New York J. Math. 6 (2000), 307–324.
- ↑ Raeburn, Iain Graph algebras. CBMS Regional Conference Series in Mathematics, 103. Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 2005. vi+113 pp. ISBN:0-8218-3660-9
- ↑ D. Drinen,Viewing AF-algebras as graph algebras, Proc. Amer. Math. Soc., 128 (2000), pp. 1991–2000.
 |

