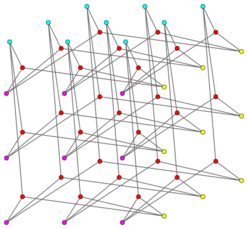
Gray graph
| Gray graph | |
|---|---|
 The Gray graph | |
| Named after | Marion Cameron Gray |
| Vertices | 54 |
| Edges | 81 |
| Radius | 6 |
| Diameter | 6 |
| Girth | 8 |
| Automorphisms | 1296 |
| Chromatic number | 2 |
| Chromatic index | 3 |
| Genus | 7 |
| Book thickness | 3 |
| Queue number | 2 |
| Properties | Cubic Semi-symmetric Hamiltonian Bipartite |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 (unpublished), then discovered independently by Bouwer 1968 in reply to a question posed by Jon Folkman 1967. The Gray graph is interesting as the first known example of a cubic graph having the algebraic property of being edge but not vertex transitive (see below).
The Gray graph has chromatic number 2, chromatic index 3, radius 6 and diameter 6. It is also a 3-vertex-connected and 3-edge-connected non-planar graph.
Construction
The Gray graph can be constructed (Bouwer 1972) from the 27 points of a 3 × 3 × 3 grid and the 27 axis-parallel lines through these points. This collection of points and lines forms a projective configuration: each point has exactly three lines through it, and each line has exactly three points on it. The Gray graph is the Levi graph of this configuration; it has a vertex for every point and every line of the configuration, and an edge for every pair of a point and a line that touch each other. This construction generalizes (Bouwer 1972) to any dimension n ≥ 3, yielding an n-valent Levi graph with algebraic properties similar to those of the Gray graph. In (Monson, Pisanski, Schulte, Ivic-Weiss 2007), the Gray graph appears as a different sort of Levi graph for the edges and triangular faces of a certain locally toroidal abstract regular 4-polytope. It is therefore the first in an infinite family of similarly constructed cubic graphs. As with other Levi graphs, it is a bipartite graph, with the vertices corresponding to points on one side of the bipartition and the vertices corresponding to lines on the other side.
Marušič and Pisanski (2000) give several alternative methods of constructing the Gray graph. As with any bipartite graph, there are no odd-length cycles, and there are also no cycles of four or six vertices, so the girth of the Gray graph is 8. The simplest oriented surface on which the Gray graph can be embedded has genus 7 (Marušič Pisanski).
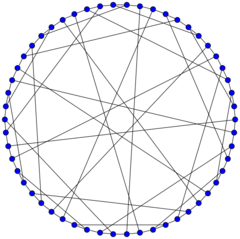
The Gray graph is Hamiltonian and can be constructed from the LCF notation:
As a Hamiltonian cubic graph, it has chromatic index three.
Algebraic properties
The automorphism group of the Gray graph is a group of order 1296. It acts transitively on the edges the graph but not on its vertices: there are symmetries taking every edge to any other edge, but not taking every vertex to any other vertex. The vertices that correspond to points of the underlying configuration can only be symmetric to other vertices that correspond to points, and the vertices that correspond to lines can only be symmetric to other vertices that correspond to lines. Therefore, the Gray graph is a semi-symmetric graph, the smallest possible cubic semi-symmetric graph.
The characteristic polynomial of the Gray graph is
Geometric properties
The Gray graph can be represented by points in the plane in such a way that adjacent vertices are at unit distance apart; that is, it is a unit distance graph. [1]
References
- Bouwer, I. Z. (1968), "An edge but not vertex transitive cubic graph", Canadian Mathematical Bulletin 11 (4): 533–535, doi:10.4153/CMB-1968-063-0. (Izak Zurk Bouwer (1933–2012) was a UNB professor. "Obituary. Izak Bouwer". Ottawa Citizen. December 28, 2012. https://ottawacitizen.remembering.ca/obituary/izak-bouwer-1065933615.)
- Bouwer, I. Z. (1972), "On edge but not vertex transitive regular graphs", Journal of Combinatorial Theory, Series B 12: 32–40, doi:10.1016/0095-8956(72)90030-5.
- "Regular line-symmetric graphs", Journal of Combinatorial Theory 3 (3): 533–535, 1967, doi:10.1016/S0021-9800(67)80069-3.
- "The Gray graph revisited", Journal of Graph Theory 35: 1–7, 2000, doi:10.1002/1097-0118(200009)35:1<1::AID-JGT1>3.0.CO;2-7.
- "The genus of the Gray graph is 7", European Journal of Combinatorics 26 (3–4): 377–385, 2005, doi:10.1016/j.ejc.2004.01.015.
- Monson, B. (2007), "Semisymmetric Graphs from Polytopes", Journal of Combinatorial Theory, Series A 114 (3): 421–435, doi:10.1016/j.jcta.2006.06.007
External links
- Weisstein, Eric W.. "Gray Graph". http://mathworld.wolfram.com/GrayGraph.html.
- The Gray Graph Is the Smallest Graph of Its Kind, from MathWorld.
 |
- ↑ Berman, Leah; Gévay, Gábor; Pisanski, Tomaž (2023). "The Gray graph is a unit-distance graph". arXiv:2312.15336.
{{cite arXiv}}: CS1 maint: missing class (link).