Gromov product

In mathematics, the Gromov product is a concept in the theory of metric spaces named after the mathematician Mikhail Gromov. The Gromov product can also be used to define δ-hyperbolic metric spaces in the sense of Gromov.

Definition

Let (X, d) be a metric space and let x, y, z ∈ X. Then the Gromov product of y and z at x, denoted (y, z)_x, is defined by

[math]\displaystyle{ (y, z)_{x} = \frac1{2} \big( d(x, y) + d(x, z) - d(y, z) \big). }[/math]

Motivation

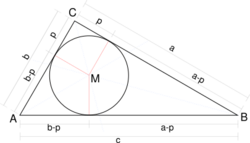
Given three points x, y, z in the metric space X, by the triangle inequality there exist non-negative numbers a, b, c such that [math]\displaystyle{ d(x,y) = a + b, \ d(x,z) = a + c, \ d(y,z) = b + c }[/math]. Then the Gromov products are [math]\displaystyle{ (y,z)_x = a, \ (x,z)_y = b, \ (x,y)_z = c }[/math]. In the case that the points x, y, z are the outer nodes of a tripod then these Gromov products are the lengths of the edges.

In the hyperbolic, spherical or euclidean plane, the Gromov product (A, B)_C equals the distance p between C and the point where the incircle of the geodesic triangle ABC touches the edge CB or CA. Indeed from the diagram c = (a – p) + (b – p), so that p = (a + b – c)/2 = (A,B)_C. Thus for any metric space, a geometric interpretation of (A, B)_C is obtained by isometrically embedding (A, B, C) into the euclidean plane.

Properties

• The Gromov product is symmetric: (y, z)_x = (z, y)_x.
• The Gromov product degenerates at the endpoints: (y, z)_y = (y, z)_z = 0.
• For any points p, q, x, y and z,

[math]\displaystyle{ d(x, y) = (x, z)_{y} + (y, z)_{x}, }[/math]

[math]\displaystyle{ 0 \leq (y, z)_{x} \leq \min \big\{ d(y, x), d(z, x) \big\}, }[/math]

[math]\displaystyle{ \big| (y, z)_{p} - (y, z)_{q} \big| \leq d(p, q), }[/math]

[math]\displaystyle{ \big| (x, y)_{p} - (x, z)_{p} \big| \leq d(y, z). }[/math]

Points at infinity

Consider hyperbolic space Hⁿ. Fix a base point p and let [math]\displaystyle{ x_\infty }[/math] and [math]\displaystyle{ y_\infty }[/math] be two distinct points at infinity. Then the limit

[math]\displaystyle{ \liminf_{x \to x_\infty \atop y \to y_\infty} (x,y)_p }[/math]

exists and is finite, and therefore can be considered as a generalized Gromov product. It is actually given by the formula

[math]\displaystyle{ (x_\infty, y_\infty)_{p} = \log \csc (\theta/2), }[/math]

where [math]\displaystyle{ \theta }[/math] is the angle between the geodesic rays [math]\displaystyle{ px_\infty }[/math] and [math]\displaystyle{ py_\infty }[/math].

δ-hyperbolic spaces and divergence of geodesics

The Gromov product can be used to define δ-hyperbolic spaces in the sense of Gromov.: (X, d) is said to be δ-hyperbolic if, for all p, x, y and z in X,

[math]\displaystyle{ (x, z)_{p} \geq \min \big\{ (x, y)_{p}, (y, z)_{p} \big\} - \delta. }[/math]

In this case. Gromov product measures how long geodesics remain close together. Namely, if x, y and z are three points of a δ-hyperbolic metric space then the initial segments of length (y, z)_x of geodesics from x to y and x to z are no further than 2δ apart (in the sense of the Hausdorff distance between closed sets).

References

• Coornaert, M.; Delzant, T.; Papadopoulos, A. (1990) (in fr), Géométrie et théorie des groupes. Les groupes hyperboliques de Gromov, Lecture Notes in Mathematics, 1441, Springer-Verlag, ISBN 3-540-52977-2 
• Kapovich, Ilya; Benakli, Nadia (2002). "Boundaries of hyperbolic groups". Combinatorial and geometric group theory (New York, 2000/Hoboken, NJ, 2001). Contemp. Math. 296. Providence, RI: Amer. Math. Soc.. pp. 39–93. 
• Väisälä, Jussi (2005). "Gromov hyperbolic spaces". Expositiones Mathematicae 23 (3): 187–231. doi:10.1016/j.exmath.2005.01.010.