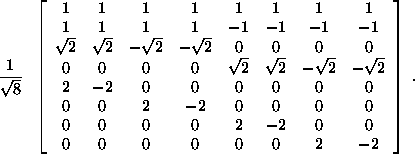Haar transform

Being the fastest of all known complete unitary transforms ( Fast Transforms), the (non-sinusoidal) Haar transform is well suited for the data compression of non-stationary (``spiky) signals, or for edge extraction in images (see Jain89). It can also be viewed as a special kind of wavelet transform.

In the Haar transform most of the coefficients are functions of only part of the signal, e.g. the (orthonormal) Haar transform matrix:

Apart from powers of , all elements are 1, -1, and 0. One can interpret the multiplication of the Haar matrix with a signal vector as sampling the signal from low to high frequencies (``sequencies). The first sample corresponds to the mean, the second to the mean difference of the first to the last four neighbour pixels, and the last four transform samples represent differences of two neighbouring pixels. Most of the transform coefficients depend only on their direct neighbours; the Haar transform thus has good high- and low-frequency response.

The following is an example of a 128-point one-dimensional signal from a physics experiment, and shows the original signal, the result of the Haar transform, and the signal that has been reconstructed from 13 transform samples.