Harmonic polynomial

In mathematics, in abstract algebra, a multivariate polynomial p over a field such that the Laplacian of p is zero is termed a harmonic polynomial. The harmonic polynomials form a vector subspace of the vector space of polynomials over the field. In fact, they form a graded subspace. For the real field, the harmonic polynomials are important in mathematical physics.

The Laplacian is the sum of second partials with respect to all the variables, and is an invariant differential operator under the action of the orthogonal group via the group of rotations.

The standard separation of variables theorem states that every multivariate polynomial over a field can be decomposed as a finite sum of products of a radial polynomial and a harmonic polynomial. This is equivalent to the statement that the polynomial ring is a free module over the ring of radial polynomials.

Examples

Consider a degree-[math]\displaystyle{ d }[/math] univariate polynomial [math]\displaystyle{ p(x) := \textstyle\sum_{k=0}^d a_k x^k }[/math]. In order to be harmonic, this polynomial must satisfy

Real harmonic polynomials in two variables up to degree 6, graphed over the unit disk.

[math]\displaystyle{ 0 = \tfrac{\partial^2}{\partial x^2} p(x) = \sum_{k=2}^d k(k-1) a_k x^{k-2} }[/math]

at all points [math]\displaystyle{ x \in \mathbb{R} }[/math]. In particular, when [math]\displaystyle{ d=2 }[/math], we have a polynomial [math]\displaystyle{ p(x) = a_0 + a_1 x + a_2 x^2 }[/math], which must satisfy the condition [math]\displaystyle{ a_2 = 0 }[/math]. Hence, the only harmonic polynomials of one (real) variable are affine functions [math]\displaystyle{ x \mapsto a_0 + a_1 x }[/math].

In the multivariable case, one finds nontrivial spaces of harmonic polynomials. Consider for instance the bivariate quadratic polynomial

[math]\displaystyle{ p(x,y) := a_{0,0} + a_{1,0} x + a_{0,1} y + a_{1,1} x y + a_{2,0} x^2 + a_{0,2} y^2, }[/math]

where [math]\displaystyle{ a_{0,0}, a_{1,0}, a_{0,1}, a_{1,1}, a_{2,0}, a_{0,2} }[/math] are real coefficients. The Laplacian of this polynomial is given by

[math]\displaystyle{ \Delta p(x,y) = \tfrac{\partial^2}{\partial x^2} p(x,y) + \tfrac{\partial^2}{\partial y^2} p(x,y) = 2(a_{2,0} + a_{0,2}). }[/math]

Hence, in order for [math]\displaystyle{ p(x,y) }[/math] to be harmonic, its coefficients need only satisfy the relationship [math]\displaystyle{ a_{2,0} = -a_{0,2} }[/math]. Equivalently, all (real) quadratic bivariate harmonic polynomials are linear combinations of the polynomials

[math]\displaystyle{ 1, \quad x, \quad y, \quad xy, \quad x^2 - y^2. }[/math]

Note that, as in any vector space, there are other choices of basis for this same space of polynomials.

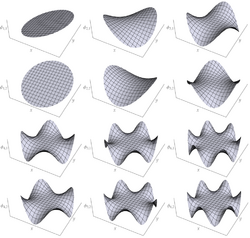
A basis for real bivariate harmonic polynomials up to degree 6 is given as follows:

[math]\displaystyle{ \begin{array}{rcl} \phi_{0} (x,y) &:=& 1 \\ \phi_{1,1}(x,y) &:=& x \\ \phi_{1,2}(x,y) &:=& y \\ \phi_{2,1}(x,y) &:=& x y \\ \phi_{2,2}(x,y) &:=& x^2-y^2 \\ \phi_{3,1}(x,y) &:=& y^3-3 x^2 y \\ \phi_{3,2}(x,y) &:=& x^3-3 x y^2 \\ \phi_{4,1}(x,y) &:=& x^3 y-x y^3 \\ \phi_{4,2}(x,y) &:=& -x^4+6 x^2 y^2-y^4 \\ \phi_{5,1}(x,y) &:=& 5 x^4 y-10 x^2 y^3+y^5 \\ \phi_{5,2}(x,y) &:=& x^5-10 x^3 y^2+5 x y^4 \\ \phi_{6,1}(x,y) &:=& 3 x^5 y-10 x^3 y^3+3 x y^5 \\ \phi_{6,2}(x,y) &:=& -x^6+15 x^4 y^2-15 x^2 y^4+y^6 \\ \end{array} }[/math]

See also

• Harmonic function
• Spherical harmonics
• Zonal spherical harmonics
• Multilinear polynomial

References

• Lie Group Representations of Polynomial Rings by Bertram Kostant published in the American Journal of Mathematics Vol 85 No 3 (July 1963) doi:10.2307/2373130