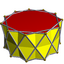
Hendecagrammic prism
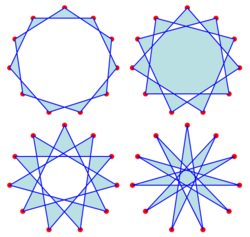
{11/2}, {11/3}, {11/4}, and {11/5}
In geometry, a hendecagrammic prism is a star polyhedron made from two identical regular hendecagrams connected by squares. The related hendecagrammic antiprisms are made from two identical regular hendecagrams connected by equilateral triangles.
Hendecagrammic prisms and bipyramids
There are 4 hendecagrammic uniform prisms, and 6 hendecagrammic uniform antiprisms. The prisms are constructed by 4.4.11/q vertex figures, ![]()
![]()
![]()
![]()
![]()
![]()
![]() Coxeter diagram. The hendecagrammic bipyramids, duals to the hendecagrammic prisms are also given.
Coxeter diagram. The hendecagrammic bipyramids, duals to the hendecagrammic prisms are also given.
| Symmetry | Prisms | |||
|---|---|---|---|---|
| D11h [2,11] (*2.2.11) |
 4.4.11/2 |
 4.4.11/3 |
 4.4.11/4 |
 4.4.11/5 |
| D11h [2,11] (*2.2.11) |
||||
Hendecagrammic antiprisms
The antiprisms with 3.3.3.3.11/q vertex figures, ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Uniform antiprisms exist for p/q>3/2,[1] and are called crossed for p/q<2. For hendecagonal antiprism, two crossed antiprisms can not be constructed as uniform (with equilateral triangles): 11/8, and 11/9.
. Uniform antiprisms exist for p/q>3/2,[1] and are called crossed for p/q<2. For hendecagonal antiprism, two crossed antiprisms can not be constructed as uniform (with equilateral triangles): 11/8, and 11/9.
Hendecagrammic trapezohedra
The hendecagrammic trapezohedra are duals to the hendecagrammic antiprisms.
| Symmetry | Trapezohedra | ||
|---|---|---|---|
| D11h [2,11] (*2.2.11) |
|||
| D11d [2+,11] (2*11) |
Error creating thumbnail: Unable to save thumbnail to destination | ||
See also
References
- ↑ Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society 79 (3): 447–457, doi:10.1017/S0305004100052440.
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). "Uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 246 (916): 401–450. doi:10.1098/rsta.1954.0003. ISSN 0080-4614.
External links
 |