Heptagonal antiprism
From HandWiki
| Uniform heptagonal antiprism | |
|---|---|
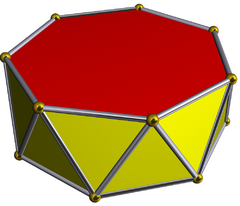
| |
| Type | Prismatic uniform polyhedron |
| Elements | F = 16, E = 28 V = 14 (χ = 2) |
| Faces by sides | 14{3}+2{7} |
| Schläfli symbol | s{2,14} sr{2,7} |
| Wythoff symbol | | 2 2 7 |
| Coxeter diagram | |
| Symmetry group | D7d, [2+,14], (2*7), order 28 |
| Rotation group | D7, [7,2]+, (722), order 14 |
| References | U77(e) |
| Dual | Heptagonal trapezohedron |
| Properties | convex |
 Vertex figure 3.3.3.7 | |
In geometry, the heptagonal antiprism is the fifth in an infinite set of antiprisms formed by two parallel polygons separated by a strip of triangles. In the case of the heptagonal antiprism, the caps are two regular heptagons. As a result, this polyhedron has 14 vertices, and 14 equilateral triangle faces. There are 14 edges where a triangle meets a heptagon, and another 14 edges where two triangles meet.
The heptagonal antiprism was first depicted by Johannes Kepler, as an example of the general construction of antiprisms.[1]
References
- ↑ Kepler, Johannes (1619), "Book II, Definition X" (in la), Harmonices Mundi, p. 49, https://archive.org/details/ioanniskepplerih00kepl/page/n65 See also illustration A, of a heptagonal antiprism.
 |
