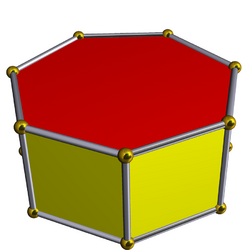
Heptagonal prism
| Heptagonal prism | |
|---|---|
 | |
| Type | Uniform polyhedron |
| Faces | 2 Heptagons 7 squares |
| Edges | 21 |
| Vertices | 14 |
| Vertex configuration | 7.4.4 |
| Wythoff symbol | 2 7 | 2 |
| Coxeter diagram | |
| Symmetry group | D7h, [7,2], (*722), order 28 |
| Rotation group | D7, [7,2]+, (722), order 14 |
| Dual polyhedron | Heptagonal bipyramid |
| Properties | Convex semiregular |
| Vertex figure | |
 | |
File:Prisma heptagonal 3D.stl In geometry, the heptagonal prism is a prism with heptagonal base. This polyhedron has 9 faces (2 bases and 7 sides), 21 edges, and 14 vertices.[1][2]
Area
The area of a right heptagonal prism with height [math]\displaystyle{ h }[/math] and with a side length of [math]\displaystyle{ L }[/math] and apothem [math]\displaystyle{ a_p }[/math] is given by:[1]
- [math]\displaystyle{ A = 7L\cdot (a_p + h) }[/math]
Volume
The volume is found by taking the area of the base, with a side length of [math]\displaystyle{ L }[/math] and apothem [math]\displaystyle{ a_p }[/math], and multiplying it by the height [math]\displaystyle{ h }[/math], giving the formula:[1]
- [math]\displaystyle{ V = \frac{7}{2}\cdot h\cdot L\cdot a_p }[/math]
This formula also works for the oblique prism due to the Cavalieri's principle.
Images
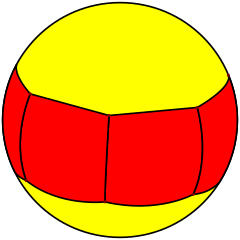
The heptagonal prism can also be seen as a tiling on a sphere:
Related polyhedra
References
- ↑ 1.0 1.1 1.2 Sapiña, R.. "Area and volume calculator of a heptagonal prism" (in es). Problemas y ecuaciones. https://www.problemasyecuaciones.com/geometria3D/volumen/prisma/heptagonal/calculadora-area-volumen-formulas-demostracion.html.
- ↑ Pugh, Anthony (1976), Polyheda: A Visual Approach, University of California Press, pp. 27, ISBN 9780520030565, https://books.google.com/books?id=IDDxpYQTR7kC&pg=PA21.
External links
 |