Hinge loss

Short description: Loss function in machine learning

The vertical axis represents the value of the Hinge loss (in blue) and zero-one loss (in green) for fixed t = 1, while the horizontal axis represents the value of the prediction y. The plot shows that the Hinge loss penalizes predictions y < 1, corresponding to the notion of a margin in a support vector machine.

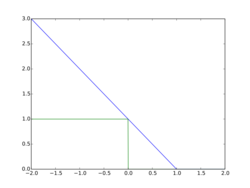
In machine learning, the hinge loss is a loss function used for training classifiers. The hinge loss is used for "maximum-margin" classification, most notably for support vector machines (SVMs).

For an intended output t = ±1 and a classifier score y, the hinge loss of the prediction y is defined as

[math]\displaystyle{ \ell(y) = \max(0, 1-t \cdot y) }[/math]

Note that [math]\displaystyle{ y }[/math] should be the "raw" output of the classifier's decision function, not the predicted class label. For instance, in linear SVMs, [math]\displaystyle{ y = \mathbf{w} \cdot \mathbf{x} + b }[/math], where [math]\displaystyle{ (\mathbf{w},b) }[/math] are the parameters of the hyperplane and [math]\displaystyle{ \mathbf{x} }[/math] is the input variable(s).

When t and y have the same sign (meaning y predicts the right class) and [math]\displaystyle{ |y| \ge 1 }[/math], the hinge loss [math]\displaystyle{ \ell(y) = 0 }[/math]. When they have opposite signs, [math]\displaystyle{ \ell(y) }[/math] increases linearly with y, and similarly if [math]\displaystyle{ |y| \lt 1 }[/math], even if it has the same sign (correct prediction, but not by enough margin).

Extensions

While binary SVMs are commonly extended to multiclass classification in a one-vs.-all or one-vs.-one fashion, it is also possible to extend the hinge loss itself for such an end. Several different variations of multiclass hinge loss have been proposed. For example, Crammer and Singer defined it for a linear classifier as

[math]\displaystyle{ \ell(y) = \max(0, 1 + \max_{y \ne t} \mathbf{w}_y \mathbf{x} - \mathbf{w}_t \mathbf{x}) }[/math],

where [math]\displaystyle{ t }[/math] is the target label, [math]\displaystyle{ \mathbf{w}_t }[/math] and [math]\displaystyle{ \mathbf{w}_y }[/math] are the model parameters.

Weston and Watkins provided a similar definition, but with a sum rather than a max:

[math]\displaystyle{ \ell(y) = \sum_{y \ne t} \max(0, 1 + \mathbf{w}_y \mathbf{x} - \mathbf{w}_t \mathbf{x}) }[/math].

In structured prediction, the hinge loss can be further extended to structured output spaces. Structured SVMs with margin rescaling use the following variant, where w denotes the SVM's parameters, y the SVM's predictions, φ the joint feature function, and Δ the Hamming loss:

[math]\displaystyle{ \begin{align} \ell(\mathbf{y}) & = \max(0, \Delta(\mathbf{y}, \mathbf{t}) + \langle \mathbf{w}, \phi(\mathbf{x}, \mathbf{y}) \rangle - \langle \mathbf{w}, \phi(\mathbf{x}, \mathbf{t}) \rangle) \\ & = \max(0, \max_{y \in \mathcal{Y}} \left( \Delta(\mathbf{y}, \mathbf{t}) + \langle \mathbf{w}, \phi(\mathbf{x}, \mathbf{y}) \rangle \right) - \langle \mathbf{w}, \phi(\mathbf{x}, \mathbf{t}) \rangle) \end{align} }[/math].

Optimization

The hinge loss is a convex function, so many of the usual convex optimizers used in machine learning can work with it. It is not differentiable, but has a subgradient with respect to model parameters w of a linear SVM with score function [math]\displaystyle{ y = \mathbf{w} \cdot \mathbf{x} }[/math] that is given by

[math]\displaystyle{ \frac{\partial\ell}{\partial w_i} = \begin{cases} -t \cdot x_i & \text{if } t \cdot y \lt 1, \\ 0 & \text{otherwise}. \end{cases} }[/math]

Plot of three variants of the hinge loss as a function of z = ty: the "ordinary" variant (blue), its square (green), and the piece-wise smooth version by Rennie and Srebro (red). The y-axis is the l(y) hinge loss, and the x-axis is the parameter t

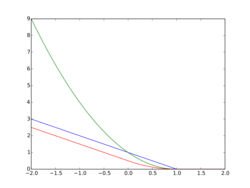
However, since the derivative of the hinge loss at [math]\displaystyle{ ty = 1 }[/math] is undefined, smoothed versions may be preferred for optimization, such as Rennie and Srebro's

[math]\displaystyle{ \ell(y) = \begin{cases} \frac{1}{2} - ty & \text{if} ~~ ty \le 0, \\ \frac{1}{2} (1 - ty)^2 & \text{if} ~~ 0 \lt ty \lt 1, \\ 0 & \text{if} ~~ 1 \le ty \end{cases} }[/math]

or the quadratically smoothed

[math]\displaystyle{ \ell_\gamma(y) = \begin{cases} \frac{1}{2\gamma} \max(0, 1 - ty)^2 & \text{if} ~~ ty \ge 1 - \gamma, \\ 1 - \frac{\gamma}{2} - ty & \text{otherwise} \end{cases} }[/math]

suggested by Zhang. The modified Huber loss [math]\displaystyle{ L }[/math] is a special case of this loss function with [math]\displaystyle{ \gamma = 2 }[/math], specifically [math]\displaystyle{ L(t,y) = 4 \ell_2(y) }[/math].

See also

• Multivariate adaptive regression spline § Hinge functions