Hypohamiltonian graph

In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G itself does not have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.
History
Hypohamiltonian graphs were first studied by (Sousselier 1963). (Lindgren 1967) cites (Gaudin Herz) and (Busacker Saaty) as additional early papers on the subject; another early work is by (Herz Duby).
(Grötschel 1980) sums up much of the research in this area with the following sentence: “The articles dealing with those graphs ... usually exhibit new classes of hypohamiltonian or hypotraceable graphs showing that for certain orders n such graphs indeed exist or that they possess strange and unexpected properties.”
Applications
Hypohamiltonian graphs arise in integer programming solutions to the traveling salesman problem: certain kinds of hypohamiltonian graphs define facets of the traveling salesman polytope, a shape defined as the convex hull of the set of possible solutions to the traveling salesman problem, and these facets may be used in cutting-plane methods for solving the problem.[1] (Grötschel 1980) observes that the computational complexity of determining whether a graph is hypohamiltonian, although unknown, is likely to be high, making it difficult to find facets of these types except for those defined by small hypohamiltonian graphs; fortunately, the smallest graphs lead to the strongest inequalities for this application.[2]
Concepts closely related to hypohamiltonicity have also been used by (Park Lim) to measure the fault tolerance of network topologies for parallel computing.
Properties
Every hypohamiltonian graph must be 3-vertex-connected, as the removal of any two vertices leaves a Hamiltonian path, which is connected. There exist n-vertex hypohamiltonian graphs in which the maximum degree is n/2, and in which there are approximately n2/4 edges.[3]
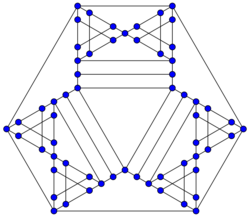
(Herz Duby) conjectured that every hypohamiltonian graph has girth 5 or more, but this was disproved by (Thomassen 1974b), who found examples with girth 3 and 4. For some time it was unknown whether a hypohamiltonian graph could be planar, but several examples are now known,[4] the smallest of which has 40 vertices.[5] Every planar hypohamiltonian graph has at least one vertex with only three incident edges.[6]
If a 3-regular graph is Hamiltonian, its edges can be colored with three colors: use alternating colors for the edges on the Hamiltonian cycle (which must have even length by the handshaking lemma) and a third color for all remaining edges. Therefore, all snarks, bridgeless cubic graphs that require four edge colors, must be non-Hamiltonian, and many known snarks are hypohamiltonian. Every hypohamiltonian snark is bicritical: removing any two vertices leaves a subgraph the edges of which can be colored with only three colors.[7] A three-coloring of this subgraph can be simply described: after removing one vertex, the remaining vertices contain a Hamiltonian cycle. After removing a second vertex, this cycle becomes a path, the edges of which may be colored by alternating between two colors. The remaining edges form a matching and may be colored with a third color.
The color classes of any 3-coloring of the edges of a 3-regular graph form three matchings such that each edge belongs to exactly one of the matchings. Hypohamiltonian snarks do not have a partition into matchings of this type, but (Häggkvist 2007) conjectures that the edges of any hypohamiltonian snark may be used to form six matchings such that each edge belongs to exactly two of the matchings. This is a special case of the Berge–Fulkerson conjecture that any snark has six matchings with this property.
Hypohamiltonian graphs cannot be bipartite: in a bipartite graph, a vertex can only be deleted to form a Hamiltonian subgraph if it belongs to the larger of the graph's two color classes. However, every bipartite graph occurs as an induced subgraph of some hypohamiltonian graph.[8]
Examples
The smallest hypohamiltonian graph is the Petersen graph (Herz Duby). More generally, the generalized Petersen graph GP(n,2) is hypohamiltonian when n is 5 (mod 6);[9] the Petersen graph is the instance of this construction with n = 5.
(Lindgren 1967) found another infinite class of hypohamiltonian graphs in which the number of vertices is 4 (mod 6). Lindgren's construction consists of a cycle of length 3 (mod 6) and a single central vertex; the central vertex is connected to every third vertex of the cycle by edges he calls spokes, and the vertices two positions away from each spoke endpoint are connected to each other. Again, the smallest instance of Lindgren's construction is the Petersen graph.
Additional infinite families are given by (Bondy 1972), (Doyen van Diest), and (Gutt 1977).
Enumeration
Václav Chvátal proved in 1973 that for all sufficiently large n there exists a hypohamiltonian graph with n vertices. Taking into account subsequent discoveries,[10] “sufficiently large” is now known to mean that such graphs exist for all n ≥ 18. A complete list of hypohamiltonian graphs with at most 17 vertices is known:[11] they are the 10-vertex Petersen graph, a 13-vertex graph and a 15-vertex graph found by computer searches of (Herz 1968), and four 16-vertex graphs. There exist at least thirteen 18-vertex hypohamiltonian graphs. By applying the flip-flop method of (Chvátal 1973) to the Petersen graph and the flower snark, it is possible to show that the number of hypohamiltonian graphs, and more specifically the number of hypohamiltonian snarks, grows as an exponential function of the number of vertices.[12]
Generalizations
Graph theorists have also studied hypotraceable graphs, graphs that do not contain a Hamiltonian path but such that every subset of n − 1 vertices may be connected by a path.[13] Analogous definitions of hypohamiltonicity and hypotraceability for directed graphs have been considered by several authors.[14]
An equivalent definition of hypohamiltonian graphs is that their longest cycle has length n − 1 and that the intersection of all longest cycles is empty. (Menke Zamfirescu) investigate graphs with the same property that the intersection of longest cycles is empty but in which the longest cycle length is shorter than n − 1. (Herz 1968) defines the cyclability of a graph as the largest number k such that every k vertices belong to a cycle; the hypohamiltonian graphs are exactly the graphs that have cyclability n − 1. Similarly, (Park Lim) define a graph to be ƒ-fault hamiltonian if the removal of at most ƒ vertices leaves a Hamiltonian subgraph. (Schauerte Zamfirescu) study the graphs with cyclability n − 2.
Notes
- ↑ (Grötschel 1977); (Grötschel 1980); (Grötschel Wakabayashi).
- ↑ (Goemans 1995).
- ↑ (Thomassen 1981).
- ↑ The existence of planar hypohamiltonian graphs was posed as an open question by (Chvátal 1973), and (Chvátal Klarner) offered a $5 prize for the construction of one. (Thomassen 1976) used Grinberg's theorem to find planar hypohamiltonian graphs of girth 3, 4, and 5 and showed that there exist infinitely many planar hypohamiltonian graphs.
- ↑ (Jooyandeh McKay), using a computer search and Grinberg's theorem. Earlier small planar hypohamiltonian graphs with 42, 57 and 48 vertices, respectively, were found by (Wiener Araya), (Hatzel 1979) and (Zamfirescu Zamfirescu).
- ↑ (Thomassen 1978).
- ↑ (Steffen 1998); (Steffen 2001).
- ↑ (Collier Schmeichel).
- ↑ (Robertson 1969) proved that these graphs are non-Hamiltonian, while it is straightforward to verify that their one-vertex deletions are Hamiltonian. See (Alspach 1983) for a classificiation of non-Hamiltonian generalized Petersen graphs.
- ↑ (Thomassen 1974a); (Doyen van Diest).
- ↑ (Aldred McKay). See also (sequence A141150 in the OEIS).
- ↑ (Skupień 1989); (Skupień 2007).
- ↑ (Kapoor Kronk); (Kronk 1969); (Grünbaum 1974); (Thomassen 1974a).
- ↑ (Fouquet Jolivet); (Grötschel Wakabayashi); (Grötschel Wakabayashi); (Thomassen 1978).
References
- Aldred, R. A. (1997), "Small hypohamiltonian graphs", J. Combinatorial Math. Combinatorial Comput. 23: 143–152, http://cs.anu.edu.au/people/bdm/papers/hypo.pdf.
- "The classification of Hamiltonian generalized Petersen graphs", Journal of Combinatorial Theory, Series B 34 (3): 293–312, 1983, doi:10.1016/0095-8956(83)90042-4.
- Bondy, J. A. (1972), "Variations of the Hamiltonian theme", Canadian Mathematical Bulletin 15: 57–62, doi:10.4153/CMB-1972-012-3.
- Busacker, R. G.; Saaty, T. L. (1965), Finite Graphs and Networks, McGraw-Hill.
- "Flip-flops in hypo-Hamiltonian graphs", Canadian Mathematical Bulletin 16: 33–41, 1973, doi:10.4153/CMB-1973-008-9.
- Chvátal, V.; Klarner, D. A.; Knuth, D. E. (1972), Selected Combinatorial Research Problems, Tech. Report STAN-CS-72-292, Computer Science Department, Stanford University, http://i.stanford.edu/pub/cstr/reports/cs/tr/72/292/CS-TR-72-292.pdf.
- Collier, J. B.; Schmeichel, E. F. (1977), "New flip-flop constructions for hypohamiltonian graphs", Discrete Mathematics 18 (3): 265–271, doi:10.1016/0012-365X(77)90130-3.
- Doyen, J.; van Diest, V. (1975), "New families of hypohamiltonian graphs", Discrete Mathematics 13 (3): 225–236, doi:10.1016/0012-365X(75)90020-5.
- Fouquet, J.-L.; Jolivet, J. L. (1978), "Hypohamiltonian oriented graphs", Cahiers Centre Études Rech. Opér. 20 (2): 171–181.
- Gaudin, T.; Herz, P.; Rossi (1964), "Solution du problème No. 29", Rev. Franç. Rech. Opérationnelle 8: 214–218.
- "Worst-case comparison of valid inequalities for the TSP", Mathematical Programming 69 (1–3): 335–349, 1995, doi:10.1007/BF01585563.
- "Hypohamiltonian facets of the symmetric travelling salesman polytope", Zeitschrift für Angewandte Mathematik und Mechanik 58: 469–471, 1977.
- "On the monotone symmetric traveling salesman problem: hypohamiltonian/hypotraceable graphs and facets", Mathematics of Operations Research 5 (2): 285–292, 1980, doi:10.1287/moor.5.2.285.
- "Hypohamiltonian digraphs", Methods of Operations Research 36: 99–119, 1980.
- "On the structure of the monotone asymmetric travelling salesman polytope I: hypohamiltonian facets", Discrete Mathematics 24: 43–59, 1981, doi:10.1016/0012-365X(81)90021-2.
- Cottle, R. W.; Kelmanson, M. L.; Korte, B., eds. (1984), "Constructions of hypotraceable digraphs", Mathematical Programming (Proc. International Congress, Rio de Janeiro, 1981), North-Holland.
- "Vertices missed by longest paths or circuits", Journal of Combinatorial Theory, Series A 17: 31–38, 1974, doi:10.1016/0097-3165(74)90025-9.
- "Infinite families of hypohamiltonian graphs", Académie Royale de Belgique, Bulletin de la Classe des Sciences, 5e Série 63 (5): 432–440, 1977.
- Häggkvist, R. (2007), Mohar, B.; Nowakowski, R. J.; West, D. B., eds., "Problem 443. Special case of the Fulkerson Conjecture", Discrete Mathematics 307 (3–5): 650–658, doi:10.1016/j.disc.2006.07.013.
- Hatzel, W. (1979), "Ein planarer hypohamiltonscher Graph mit 57 Knoten", Math. Ann. 243 (3): 213–216, doi:10.1007/BF01424541.
- Herz, J. C. (1968), "Sur la cyclabilité des graphes", Computers in Mathematical Research, North-Holland, pp. 97–107.
- Herz, J. C.; Duby, J. J.; Vigué, F. (1967), "Recherche systématique des graphes hypohamiltoniens", Theory of Graphs: International Symposium, Rome 1966, Paris: Gordon and Breach, pp. 153–159.
- Jooyandeh, Mohammadreza (2017), "Planar Hypohamiltonian Graphs on 40 Vertices", Journal of Graph Theory 84 (2): 121–133, doi:10.1002/jgt.22015, Bibcode: 2013arXiv1302.2698J.
- Kapoor, S. F.; Kronk, H. V.; Lick, D. R. (1968), "On detours in graphs", Canadian Mathematical Bulletin 11 (2): 195–201, doi:10.4153/CMB-1968-022-8.
- Kronk, H. V. (1969), "Does there exist a hypotraceable graph?", American Mathematical Monthly 76 (7): 809–810, doi:10.2307/2317879.
- Lindgren, W. F. (1967), "An infinite class of hypohamiltonian graphs", American Mathematical Monthly 74 (9): 1087–1089, doi:10.2307/2313617.
- Máčajová, E.; Škoviera, M. (2007), "Constructing hypohamiltonian snarks with cyclic connectivity 5 and 6", Electronic Journal of Combinatorics 14 (1): R14, doi:10.37236/936, http://www.combinatorics.org/Volume_14/Abstracts/v14i1r18.html.
- Menke, B.; Zamfirescu, T. I.; Zamfirescu, C. M. (1998), "Intersections of longest cycles in grid graphs", Journal of Graph Theory 25 (1): 37–52, doi:10.1002/(SICI)1097-0118(199705)25:1<37::AID-JGT2>3.0.CO;2-J.
- Mohanty, S. P.; Rao, D. (1981), "A family of hypo-hamiltonian generalized prisms", Combinatorics and Graph Theory, Lecture Notes in Mathematics, 885, Springer-Verlag, pp. 331–338, doi:10.1007/BFb0092278, ISBN 978-3-540-11151-1.
- Park, J.-H.; Lim, H.-S.; Kim, H.-C. (2007), "Panconnectivity and pancyclicity of hypercube-like interconnection networks with faulty elements", Theoretical Computer Science 377 (1–3): 170–180, doi:10.1016/j.tcs.2007.02.029.
- Robertson, G. N. (1969), Graphs minimal under girth, valency and connectivity constraints, Ph. D. thesis, Waterloo, Ontario: University of Waterloo.
- Schauerte, Boris; Zamfirescu, C. T. (2006), "Regular graphs in which every pair of points is missed by some longest cycle", An. Univ. Craiova Ser. Mat. Inform. 33: 154–173.
- "Exponentially many hypohamiltonian graphs", Graphs, Hypergraphs and Matroids III (Proc. Conf. Kalsk 1988), Zielona Góra: Higher College of Engineering, 1989, pp. 123–132. As cited by (Skupień 2007).
- Skupień, Z. (2007), "Exponentially many hypohamiltonian snarks", 6th Czech-Slovak International Symposium on Combinatorics, Graph Theory, Algorithms and Applications, Electronic Notes in Discrete Mathematics, 28, pp. 417–424, doi:10.1016/j.endm.2007.01.059.
- Sousselier, R. (1963), "Problème no. 29: Le cercle des irascibles", Rev. Franç. Rech. Opérationnelle 7: 405–406.
- Steffen, E. (1998), "Classification and characterizations of snarks", Discrete Mathematics 188 (1–3): 183–203, doi:10.1016/S0012-365X(97)00255-0.
- Steffen, E. (2001), "On bicritical snarks", Math. Slovaca 51 (2): 141–150.
- "Hypohamiltonian and hypotraceable graphs", Discrete Mathematics 9: 91–96, 1974a, doi:10.1016/0012-365X(74)90074-0.
- "On hypohamiltonian graphs", Discrete Mathematics 10 (2): 383–390, 1974b, doi:10.1016/0012-365X(74)90128-9.
- "Planar and infinite hypohamiltonian and hypotraceable graphs", Discrete Mathematics 14 (4): 377–389, 1976, doi:10.1016/0012-365X(76)90071-6.
- "Hypohamiltonian graphs and digraphs", Theory and applications of graphs (Proc. Internat. Conf., Western Mich. Univ., Kalamazoo, Mich., 1976), Lecture Notes in Mathematics, 642, Berlin: Springer-Verlag, 1978, pp. 557–571.
- "Planar cubic hypo-Hamiltonian and hypotraceable graphs", Journal of Combinatorial Theory, Series B 30: 36–44, 1981, doi:10.1016/0095-8956(81)90089-7.
- Wiener, Gábor; Araya, Makoto (2009), The ultimate question, Bibcode: 2009arXiv0904.3012W.
- Zamfirescu, C. T.; Zamfirescu, T. I. (2007), "A planar hypohamiltonian graph with 48 vertices", Journal of Graph Theory 55 (4): 338–342, doi:10.1002/jgt.20241.
External links
- Weisstein, Eric W.. "Hypohamiltonian Graph". http://mathworld.wolfram.com/HypohamiltonianGraph.html.
 |
